4

I have a 3d plot with oddly angled tick marks. Whether it's due to the viewing angle being unexpected or some other reason, the tick marks on the bottom axes are angled up along the sides rather than in to the plane. In order to fix this, I'd like to manually change the tick angle back to what it should be, but I can't find the setting that controls tick direction. Any help?

Edit:

Here is a simple example that illustrates the problem: suppose I plot

Plot3D[x + y, {x, 0, 1}, {y, 0, 1}]

At first, the tick marks on the x and y axes are in the x-y plane. However, if I rotate the point of view, I fairly quickly (around ViewPoint -> {2.22811, -2.31877, 1.05302}) find that the ticks switch from being in the x-y plane to pointing up along the z axis. I want to stop it from doing that, so that the ticks stay in the x-y plane for other choices of ViewPoint. This really seems like the sort of thing there ought to be a setting for.

Matt
  • 743
  • 5
  • 14
  • 1
    Perhaps you can find a solution here http://mathematica.stackexchange.com/questions/9530/how-to-align-rotated-tick-labels . May be your problem is different. In that case can you post the example you are having problem with. – Sumit Jun 26 '13 at 06:26
  • 1
    That explains how to change the properties of tick labels, which is fairly well explained in the documentation anyway. I'm asking how to change the tick direction itself, which is rather straightforwardly a different problem. Unless the same method applies? – Matt Jun 26 '13 at 15:46
  • It would be helpful to show your code. – Corey Kelly Jun 27 '13 at 11:35

1 Answers1

1

Since I don't find an way to modify the Tics orientation, I use a zero length for the Tics and put my custom marks as Epilog.

xmin = 0; xmax = 7.5;
ymin = -1; ymax = 1;

txl = 0.1; txr = \[Pi]/4; txg = 1.5;
tyl = 0.1; tyr = 0; tyg = .5;
(*length, rotation and gap for x and y ticks*)

tic = {Table[ Line[{{tx, 0}, {tx + txl*Cos[txr], txl*Sin[txr]}}], {tx, xmin, xmax, txg}],  Table[Line[{{0, ty}, {tyl*Cos[tyr], ty + tyl*Sin[tyr]}}], {ty, ymin, ymax, tyg}]};
(*creating the marks*)

ticlabel = {Table[{tx, tx, 0}, {tx, xmin, xmax, txg}], Table[{ty, ty, 0}, {ty, ymin, ymax, tyg}]};
(*you can choose any tick label here - it is the second element of the tables*)

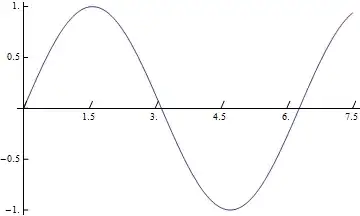
Plot[Sin[x], {x, xmin, xmax}, Ticks -> ticlabel, Epilog -> tic]

And this is how it looks.

tics2

For 3D

Thanks @Jens for pointing out. For 3D one can go with same prescription. Here instead of Epilog lets use Graphics3D for creating the tics and Show to combine it with the main plot.

xmin = 0; xmax = 7.5;
ymin = -1; ymax = 2;
zmin = -1; zmax = 1;

txl = 0.2; txr =3 \[Pi]/4; txg = 1.5;
txy = ymin; txz = zmin; (*y and z position for x tics*)
tyl = 0.2; tyr = 0; tyg = .5;
tyz = zmin; tyx = xmax;
tzl = 0.2; tzr = 0; tzg = .5;
tzx = xmin; tzy = ymin;
(*length,rotation and gap for x, y and z ticks*)
(*you can add two rotation angles as well for each tick*)

tic = {Table[Line[{{tx, txy, txz}, {tx + txl*Cos[txr], txl*Sin[txr] + txy,txz}}], {tx, xmin, xmax, txg}], 
Table[Line[{{tyx, ty, tyz}, {tyl*Cos[tyr] + tyx, ty + tyl*Sin[tyr],tyz}}], {ty, ymin, ymax, tyg}], 
Table[Line[{{tzx, tzy, tz}, {tzl + tzx, tzy, tz}}], {tz, zmin, zmax, tzg}]};
(*creating the marks*)

ticlabel = {Table[{tx, tx, 0}, {tx, xmin, xmax, txg}], 
Table[{ty, ty, 0}, {ty, ymin, ymax, tyg}], 
Table[{tz, tz, 0}, {tz, zmin, zmax, tzg}]};
(*you can choose any tick label here-it is the second element of the tables*)

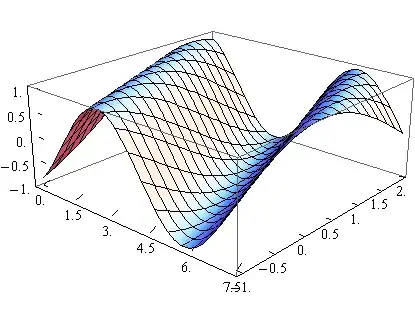
Show[Plot3D[Sin[x + y], {x, xmin, xmax}, {y, ymin, ymax},Ticks -> ticlabel], Graphics3D[tic]]

And the output is

tics3

You can go with Graphics + Show combination for 2D also.

Sumit
  • 15,912
  • 2
  • 31
  • 73