Arrange a system of differential equations to standard state-space equation form

Question

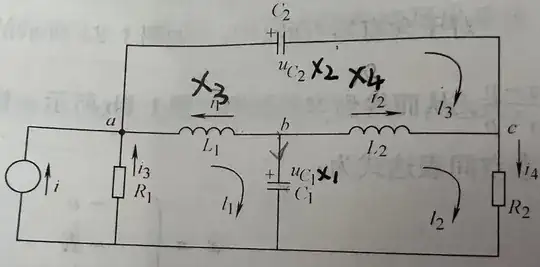
I want to model an electrical circuit in the form of state-space equations, and I want to use Mathematica to solve the final equations, the circuit equations (from Kirchhoff's law) are shown below, and the upper point indicates differential calculation.

$$ \dot{x}=\frac{d x}{d t} $$

Kirchhoff's current law:

$$ \begin{array}{c}i+i_{3}+x_{3}-C_{2} \dot{x}_{2}=0 \\C_{1} \dot{x}_{1}+x_{3}+x_{4}=0 \\C_{2} \dot{x}_{2}+x_{4}-i_{4}=0\end{array} $$

Kirchhoff's voltage law:

$$ \begin{array}{c}-L_{1} \dot{x}_{3}+x_{1}+R_{1} i_{3}=0 \\-x_{1}+L_{2} \dot{x}_{4}+R_{2} i_{4}=0 \\L_{2} \dot{x}_{4}-L_{1} \dot{x}_{3}-x_{2}=0\end{array} $$

i.e.

eq1 = i + i3 + x3[t] - C2*x2'[t] == 0
eq2 = C1*x1'[t] + x3[t] + x4[t] == 0
eq3 = C2*x2'[t] + x4[t] - i4 == 0
eq4 = -L1*x3'[t] + x1[t] + R1*i3 == 0
eq5 = -x1[t] + L2*x4'[t] + R2*i4 == 0
eq6 = L2*x4'[t] - L1*x3'[t] - x2[t] == 0

I can only simplify these equations with pen and paper, like first I eliminate two variables i3 and i4

$$ \begin{array}{l}\dot{x}_{1}=-\frac{1}{C_{1}} x_{3}-\frac{1}{C_{1}} x_{4} \\R_{1} C_{2} \dot{x}_{2}-L_{1} \dot{x}_{3}=-x_{1}+R_{1} x_{3}+R_{1} i \\R_{2} C_{2} \dot{x}_{2}+L_{2} \dot{x}_{4}=x_{1}-R_{2} x_{4} \\-L_{1} \dot{x}_{3}+L_{2} \dot{x}_{4}=x_{2}\end{array}$$

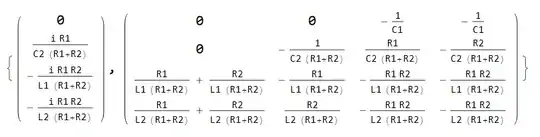
And then arrange them in a standard state-space equation form:

$$ \left(\begin{array}{l}\dot{x}_{1} \\\dot{x}_{2} \\\dot{x}_{3} \\\dot{x}_{4}\end{array}\right)=\left(\begin{array}{cccc}0 & 0 & -\frac{1}{C_{1}} & -\frac{1}{C_{1}} \\0 & -\frac{1}{C_{2}\left(R_{1}+R_{2}\right)} & \frac{R_{1}}{C_{2}\left(R_{1}+R_{2}\right)} & -\frac{R_{2}}{C_{2}\left(R_{1}+R_{2}\right)} \\\frac{1}{L_{1}} & -\frac{R_{1}}{L_{1}\left(R_{1}+R_{2}\right)} & -\frac{R_{1} R_{2}}{L_{1}\left(R_{1}+R_{2}\right)} & -\frac{R_{1} R_{2}}{L_{1}\left(R_{1}+R_{2}\right)} \\\frac{1}{L_{2}} & -\frac{R_{2}}{L_{2}\left(R_{1}+R_{2}\right)} & -\frac{R_{1} R_{2}}{L_{2}\left(R_{1}+R_{2}\right)} & -\frac{R_{1} R_{2}}{L_{2}\left(R_{1}+R_{2}\right)}\end{array}\right)\left(\begin{array}{l}x_{1} \\x_{2} \\x_{3} \\x_{4}\end{array}\right)+\left(\begin{array}{c}0 \\\frac{R_{1}}{C_{2}\left(R_{1}+R_{2}\right)} \\-\frac{R_{1} R_{2}}{L_{1}\left(R_{1}+R_{2}\right)} \\-\frac{R_{1} R_{2}}{L_{2}\left(R_{1}+R_{2}\right)}\end{array}\right) i $$

I've searched a lot, but I can't find any reference to help me.

Answer 1

Combine Eliminate and Solve is OK, but it's simpler to use hidden syntax of Solve:

vars = {x1[t], x2[t], x3[t], x4[t]};
sol = Solve[{eq1, eq2, eq3, eq4, eq5, eq6}, D[vars, t], {i3, i4}]

The matrix can then be easily obtained with CoefficientArray:

coef = CoefficientArrays[sol[[1, All, -1]], vars]
MatrixForm /@ coef

Answer 2

I've figured it out... Although it is a set of differential equations, however, the simplifying process doesn't involve differential or integral calculation, so I just define the higher order part like x1'[t] as x1d. The equations can be written as:

eq1 = i + i3 + x3 - C2*x2d == 0
eq2 = C1*x1d + x3 + x4 == 0
eq3 = C2*x2d + x4 - i4 == 0
eq4 = -L1*x3d + x1 + R1*i3 == 0
eq5 = -x1 + L2*x4d + R2*i4 == 0
eq6 = L2*x4d - L1*x3d - x2 == 0
eqns = eq1 && eq2 && eq3 && eq4 && eq5 && eq6

Firstly, use 'Elimination' to eliminate i3 and i4:

Eliminate[eqns, {i3, i4}]

output[52]:

i R1 == C1 R1 x1d + C2 R1 x2d + C2 R2 x2d - L1 x3d + R1 x4 + R2 x4 + 
   L2 x4d && x1 == C2 R2 x2d + R2 x4 + L2 x4d && 
 x2 == -L1 x3d + L2 x4d && x3 == -C1 x1d - x4

Then just use Solve to separate x1d...x4d from these equations

MatrixForm[Solve[%52, {x1d, x2d, x3d, x4d}]]

output

$$ \left\{\left\{\text{x1d}\to -\frac{\text{x3}+\text{x4}}{\text{C1}},\text{x2d}\to -\frac{-i \text{R1}-\text{R1} \text{x3}+\text{R2} \text{x4}+\text{x2}}{\text{C2} (\text{R1}+\text{R2})},\text{x3d}\to -\frac{i \text{R1} \text{R2}+\text{R1} \text{R2} \text{x3}+\text{R1} \text{R2} \text{x4}-\text{R1} \text{x1}+\text{R1} \text{x2}-\text{R2} \text{x1}}{\text{L1} (\text{R1}+\text{R2})},\text{x4d}\to -\frac{i \text{R1} \text{R2}+\text{R1} \text{R2} \text{x3}+\text{R1} \text{R2} \text{x4}-\text{R1} \text{x1}-\text{R2} \text{x1}-\text{R2} \text{x2}}{\text{L2} (\text{R1}+\text{R2})}\right\}\right\} $$