Confusion in Eigenvalue and eigenfunction distribution using NDEigensystem

Question

I have been using NDEigensystem to solve the Schrodinger equation for different potentials. However, whenever the potential has its minimum in the negative y-axis, the eigenvalues and eigenfunction don't come in a sorted manner. This creates a huge problem when I use these results for further calculations.

I want to know how to make NDEigensystem give me eigenvalues and eigenfunctions in an increasing manner. Below is my attached code and comparison graph of sorted and unsorted results.

L = 10.0; h = 1;
V[x_] := x^2 - 8;
H = -1/2 *Laplacian[u[x], {x}] + V[x]*u[x];
{vals, funs} = NDEigensystem[{H, DirichletCondition[u[x] == 0, True]}, u[x], {x, -L, L}, 50, Method -> {"PDEDiscretization" -> {"FiniteElement", {"MeshOptions" -> {MaxCellMeasure -> 0.001}}}}];

The eigenvalues come as given below(one +ve, one -ve). I think NDEigensystem is calculating eigenvalues in both directions.

vals={-0.221825, 1.19239, -1.63604, 2.6066, -3.05025, 4.02082, -4.46447,5.43503, -5.87868,6.84924, -7.29289, 8.26346, 9.67767, 11.0919,12.5061, 13.9203, 15.3345, 16.7487, 18.163, 19.5772}

which is why I use Sort to rearrange them which solves the problem, and by intuition, I should Sort the eigenfunctions(funs) also. But how to sort them?? is there any way?

it looks like eigenvalues are arranged in increasing absolute values. When you sort them, obviously then you have to keep track of the associated eigenfunctions at same time. otherwise they will become out of order. Is this what you are asking how to do? — Nasser, Dec 06 '22 at 06:42
From the Details and Options section of the documentation: “Eigenvalues are sorted in order of increasing absolute value.” — Ghoster, Dec 06 '22 at 06:55
@Nasser, Yes, that is the question. But how to do that? How to sort the eigenstates? — user444, Dec 06 '22 at 07:31
@Ghoster, that should have been the case. but here in this problem they come as mentioned above. — user444, Dec 06 '22 at 07:32
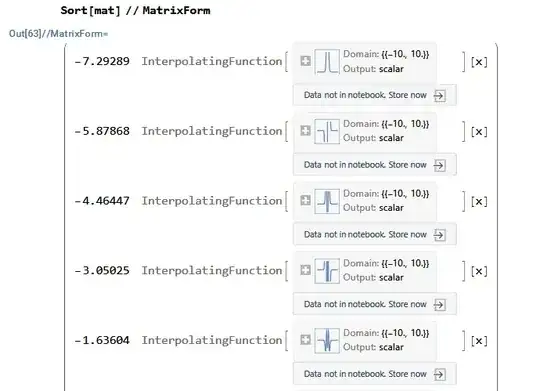
{sortedVals, sortedFuns} = Transpose[SortBy[Transpose[{vals, funs}], First]]; ? — Julien Kluge, Dec 06 '22 at 07:40
that should have been the case. but here in this problem they come as mentioned above Your list of eigenvalues IS in order of increasing absolute value. — Ghoster, Dec 06 '22 at 15:38

score 3 · Accepted Answer · answered Dec 06 '22 at 07:39

How to sort the eigenstates?

If you have matrix mat = {{1, a}, {9, b}, {4, c}} then Sort will automatically sort by first column and will arrange all rows. So

(mat = {{1, a}, {9, b}, {4, c}}) // MatrixForm

Mathematica graphics

Sort[mat] // MatrixForm

Mathematica graphics

So do the same for your case. Let the eigenvalues be the first column and the eigenfunctions be the second column and call Sort.

{vals, funs} = 
  NDEigensystem[{H, DirichletCondition[u[x] == 0, True]}, 
   u[x], {x, -L, L}, 50, 
   Method -> {"PDEDiscretization" -> {"FiniteElement", {"MeshOptions" \
-> {MaxCellMeasure -> 0.001}}}}];
mat = Transpose[{vals, funs}];
Sort[mat]

Now the eigenvalues are sorted but at the same time the eigenfunctions are kept with the same eigenvalue as the sorting is made.

Confusion in Eigenvalue and eigenfunction distribution using NDEigensystem

1 Answers1