How to get actual triangles from DelaunayTriangulation[]?

Question

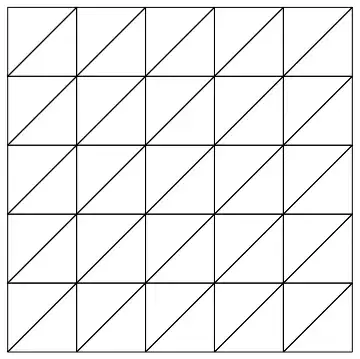
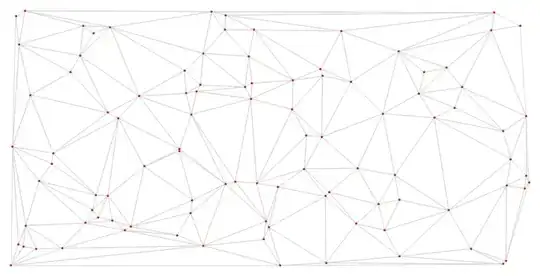
The ComputationalGeometry package has a DelaunayTriangulation[] function. It returns a list of points connected to each point, ordered counterclockwise.

Example:

showTriangulation[tri_, opt : OptionsPattern[]] := 
 Graphics[GraphicsComplex[points, Line /@ Thread /@ tri], opt]

points = Tuples[Range[0, 5, 1], 2];

tri = DelaunayTriangulation[points];
showTriangulation[tri]

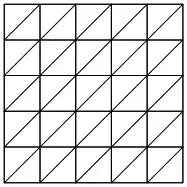
Question: How can I obtain a list of all triangles instead?

---

My first naive first try doesn't work correctly:

makeTriangles[points_] := 
 Flatten[Function[{p, list}, 
    Prepend[#, p] & /@ Partition[list, 2, 1, {1, 1}]] @@@ 
   DelaunayTriangulation[points], 1] (* doesn't work *)

GraphicsComplex[points, Line@makeTriangles[points]] // Graphics

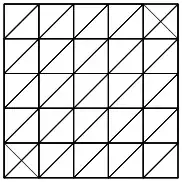
Why does it give an incorrect result?

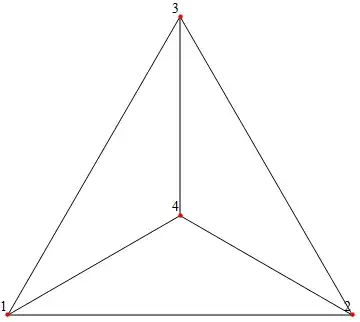
This function simply takes all points $\{A, B, C, D, \ldots\}$ connected to a point $P$, and constructs the triangles $PAB, PBC, PCD, \ldots$. Since $A,B,C,...$ are in counterclockwise order, I assumed all these would be valid triangles. But take the following case:

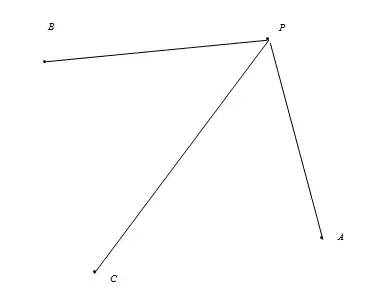
$PAB$ will not be a valid triangle, even though $ABC$ are in counterclockwise order.

Answer 1

It might be easier to use TriangularSurfacePlot3D to find the Delaunay triangulation of the points. For example,

Needs["ComputationalGeometry`"];
triangles[points_] := Module[{pl},
  pl = TriangularSurfacePlot[ArrayPad[points, {{0, 0}, {0, 1}}]];
  Cases[pl, Polygon[a_] :> Flatten[(Position[points, #[[{1, 2}]]] & /@ a)], 
    Infinity]]

Graphics[GraphicsComplex[points, {EdgeForm[Black], FaceForm[],    
  Polygon[triangles[points]]}]]

produces this:

---

If we use the approach in the original question, each valid triangle should appear exactly trice in the list, so a way to extract the triangles from the result of DelaunayTriangulation would be

Needs["ComputationalGeometry`"];
triangles2[points_] := Module[{tr, triples},
  tr = DelaunayTriangulation[points];
  triples = Flatten[Function[{v, list},
      Switch[Length[list],
        (* account for nodes with connectivity 2 or less *)
        1, {},
        2, {Flatten[{v, list}]}, 
        _, {v, ##} & @@@ Partition[list, 2, 1, {1, 1}]
      ]
    ] @@@ tr, 1];
  Cases[GatherBy[triples, Sort], a_ /; Length[a] == 3 :> a[[1]]]]

Edit

I've moved Needs["ComputationalGeometry`"] outside of the function definition of triangles. As Szabolcs correctly remarked in his comments, putting Needs["ComputationalGeometry`"] inside the definition will cause shadowing problems because of the creation of the symbol Global`DelaunayTriangulation

Edit 2

Apparently ListDensityPlot uses a Delaunay triangulation as well, and is much faster than TriangularSurfacePlot, so the first part of this answer could be made much more efficient by rewriting it according to

triangles1[points_] := Module[{pl},
  pl = ListDensityPlot[ArrayPad[points, {{0, 0}, {0, 1}}]];
  Cases[pl, Polygon[a_] :> a, Infinity][[1]]]

Note that since ListDensityPlot returns a GraphicsComplex and it keeps the order of the points the same, the index lists for the polygons can extracted directly from the plot without having to lookup the indices of the vertices in points.

Answer 2

In Mathematica 10, you can use DelaunayMesh on a set of points. This returns a MeshRegion. You can use MeshCoordinates to return a list of coordinates of the points (should be the same as the initial set of points) and then MeshCells to return the triangles.

See Interactive Computational Geometry for more details.

Answer 3

Update

It seems that the simplest way to find Delaunay triangles is to read them off from Voronoi diagram. Here is only two lines of code:

Needs["ComputationalGeometry`"]  

listSow[{pt_, list_}] := Scan[Sow[pt, #] &, list];

DelaunayTriangles[pts_] := Select[
Last@Reap@Scan[listSow, Last@VoronoiDiagram[pts]], (Length[#] == 3) &]

Application is as follows:

npts = 100;
pts = Transpose@{RandomReal[{0, 2}, npts], RandomReal[{0, 1}, npts]};

Graphics@GraphicsComplex[pts,
{{FaceForm@None, EdgeForm@LightGray,Polygon/@ DelaunayTriangles[pts]}, {Red, Point@Range@npts}}]

Obsolete part

I just would like to notice that the part of Heike's answer, there DelaunayTriangulation is used, is not completely correct. Let me demonstrate it with a simple example:

Needs["ComputationalGeometry`"]  
pts = {{0, 0}, {1, 0}, {1/2, Sqrt[3]/2}, {1/2, 1/(2 Sqrt[3])}};  
delaunayGraph = DelaunayTriangulation[pts];

Let's now find the graph edges

edges = Join@@Table[Thread[{v, Select[delaunayGraph[[v, 2]], # > v &]}], {v, 1, Length[pts] - 1}]; 

and depict them

Graphics[{Line@pts[[#]] & /@ edges, {Red, PointSize -> Medium, Point[pts]},  
FontSize -> 14, MapIndexed[Inset[First@#2, #1, {Right, Bottom}] &, pts]}]

It is easy to see that the triangle {1,2,3} appears also thrice in Heike's list.

triangles2[pts]  
(* {{1, 2, 4}, {1, 4, 3}, {1, 3, 2}, {2, 3, 4}} *)

Probably, the triangular convex hull is the only such example. In any case here is my "brute force" solution:

area[v1_, v2_] := Det[Subtract @@@ {v1, v2}]  

findSmallest[{a_, b_}, list_] := First@SortBy[list, Abs@area[pts[[{#, b}]], pts[[{a, b}]]] &]

findPartners[{a_, b_}, list_] := findSmallest[{a, b}, #] & /@  
GatherBy[list, Sign@area[pts[[{#, b}]], pts[[{a, b}]]] &] 

tri[a_, b_] := Sequence @@ (Sort[{a, #, b}] & /@ 
 findPartners[{a, b}, Intersection[delaunayGraph[[a, 2]], delaunayGraph[[b, 2]]]]);

triples = Union[tri @@@ edges]  
(* {{1, 2, 4}, {1, 3, 4}, {2, 3, 4}} *)

The idea is as follows: firstly, for an every edge {a,b} we find additional vertices attached to it (they form triangle with the edge), see Intersection in tri. Then we gather these vertices according to parts of the plane divided by the edge linear continuation, see GatherBy in findPartners. Finally, we find the triangle of the smallest area in each part of the plane, see SortBy in findSmallest.

Answer 4

How about

triangles[vertices_] := 
    DeleteDuplicates[Sort /@ Flatten[Partition[#[[2]], 2, 1] /.
                     {x_Integer, y_Integer} :> {#[[1]], x, y} & /@ vertices, 1]]

(using Partition[] to make lists of triangles with three vertices instead of four)

In[95]:= triangles[tri]
Out[95]= {{1,7,8},{1,2,8},{2,8,9},{2,3,9},{3,9,10},{3,4,10},{4,10,11},{4,5,11},{5,11,12},{5,6,12},{7,13,14},{7,8,14},{8,14,15},{8,9,15},{9,15,16},{9,10,16},{10,16,17},{10,11,17},{11,17,18},{11,12,18},{13,19,20},{13,14,20},{14,20,21},{14,15,21},{15,21,22},{15,16,22},{16,22,23},{16,17,23},{17,23,24},{17,18,24},{19,25,26},{19,20,26},{20,26,27},{20,21,27},{21,27,28},{21,22,28},{22,28,29},{22,23,29},{23,29,30},{23,24,30},{25,31,32},{25,26,32},{26,32,33},{26,27,33},{27,33,34},{27,28,34},{28,34,35},{28,29,35},{29,35,36},{29,30,36}}

Graphics[{FaceForm[None], EdgeForm[Thickness[Medium]],
   (* the triangles *) GraphicsComplex[points, Polygon[triangles[tri]]],
   (* and their labels *) MapIndexed[Text[#2[[1]], Mean[#1 /. Thread[Range@Length@tri -> points]]] &, triangles[tri]]}]