What could be an efficient SublistQ command?

Question

I know about SubsetQ but I could not find SublistQ such that SublistQ[a, b] would be true if and only if b is a sublist of a (that is, a has form Join[x, b, y] for some x, y).

I came up with

mySublistQ[a_, b_] := 
 With[{lb = Length[b] - 1}, 
  lb < 0 \[Or] 
   Or @@ Map[
     With[{try = Drop[a, First[#]]}, 
       Length[try] >= lb \[And] Take[try, lb] == Rest[b]] &, Position[a, First[b]]]]

Can one do better?

Answer 1

Consider the following functions:

Clear[sublistQ]; 
sublistQ[a_, b_] := 
 Catch[MovingMap[If[# == b, Throw[True], False] &, a, Length@b - 1]; 
  False]
Clear[sublistQ2];
sublistQ2[a_, b_] := MatchQ[a, {x___, Sequence @@ b, y___}]

I also considered @Syed's LongestCommonSubsequence method out of curiosity and added the SequenceCount function

 sublistQ3[a_, b_] := SequenceCount[a, b] > 0

---

Test example and benchmark :

Consider the question of whether the first $n$ digits of $ \exp(1)=e$ appear in the first $m$ digits of $\pi$:

Below we consider 6 digits of the Euler number $ \exp(1)=e$ and at most $5\times10^7$ digits of $\pi$

a = First@RealDigits[N[Pi, 5*10^7]];
b = First@RealDigits[N[E, 6]];

The image below shows the evolution of how long each method takes to check whether the statement is True or False. Note that the answer is always True for the ranges I took so theoretically a fast algorithm would take a near constant time.

tab1 = Table[{n, First@AbsoluteTiming@sublistQ[a[[1 ;; n]], b]}, {n, 
    Subdivide[5*10^5, 5*10^7, 10]}];
tab2 = Table[{n, First@AbsoluteTiming@sublistQ2[a[[1 ;; n]], b]}, {n, 
    Subdivide[510^5, 510^7, 10]}];
tab3 = Table[{n, First@AbsoluteTiming@mySublistQ[a[[1 ;; n]], b]}, {n,
     Subdivide[510^5, 510^7, 10]}];
tab4 = Table[{n, First@AbsoluteTiming@sublistQ3[a[[1 ;; n]], b]}, {n, 
    Subdivide[510^5, 510^7, 10]}];

I also checked that they all agreed on true or false.

Timing as a function of the size of the first list for which we ask whether the second list is a member of. The answer is True for each point below. The scale is linear.

---

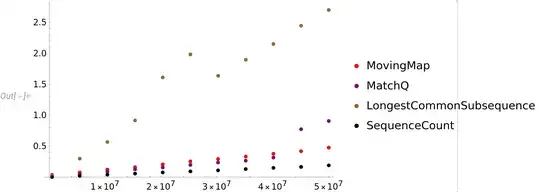
Consider now fixing the big list and increasing the length of the small list:

b = First@RealDigits[N[E, 7]];
a = First@RealDigits[N[Pi, 5*10^7]];
tab1 = Table[{n, First@AbsoluteTiming@sublistQ[a, b[[1 ;; n]]]}, {n, 
    2, 7}];
tab2 = Table[{n, First@AbsoluteTiming@sublistQ2[a, b[[1 ;; n]]]}, {n, 
    2, 7}];
tab3 = Table[{n, First@AbsoluteTiming@mySublistQ[a, b[[1 ;; n]]]}, {n,
     2, 7}];
tab4 = Table[{n, First@AbsoluteTiming@sublistQ3[a, b[[1 ;; n]]]}, {n, 
    2, 7}];
ListLogPlot[{tab1, tab2, tab3, tab4}, 
 PlotStyle -> {Red, Purple, Brown, Black}, 
 PlotLegends -> {MovingMap, MatchQ, LongestCommonSubsequence, 
   SequenceCount}]

Timing as a function of the size of the second list for which we ask whether the first list contains it. The vertical scale (y-axis) is logarithmic.

---

Now consider the case of a long subsequence that is not present:

b = First@RealDigits[N[E, 8]];
a = First@RealDigits[N[Pi, 5*10^7]];

Timing below in seconds

MovingMap

 {50.1696, False}

LongestCommonSubsequence

{3.70687, False}

MatchQ

{1.59695, False}

SequenceCount

{0.109687, False}

Answer 2

subListQ[lst_, sublst_]:=!(SequenceCases[lst, sublst,1]==={})

Examples:

lst1={1,2,3,4,6,7};
lst2={2,3,4};
lst3={2,3,4,7};
subListQ[lst1,lst2]
subListQ[lst1,lst3]
subListQ[lst1,lst1]
True
False
True

Answer 3

There is a rich collection of Sequence* functions in Mathematica to do this. Let's create a minimal example and use SubsetQ for comparison later on.

a = Range[1, 20];
b = {4, 2, 3};
c = Range[11, 15];
{SubsetQ[a, b], SubsetQ[a, c]}

{True, True}

Now define:

mySublistQ[a_, b_] := LongestCommonSubsequence[a, b] == b
{mySublistQ[a, b], mySublistQ[a, c]}

{False, True}

---

Sequence* functions can be a bit slow at times. An alternative approach using DeleteCases could be:

f2[a_, b_] := 
 MemberQ[Partition[DeleteCases[a, _?(! MemberQ[b, #] &)], Length@b], 
  b]
{f2[a, b], f2[a, c]}

{False, True}

This would still not be a comprehensive solution for multiple/overlappping copies

---

The more natural way to find overlaps and multiple copies (if required) can be done with Sequence* functions. Consider:

a = {2, 2, 1, 4, 1, 4, 1, 2, 1, 4, 1, 3}
b = {1, 4, 1}
SequenceCases[a, b, Overlaps -> All]

{{1, 4, 1}, {1, 4, 1}, {1, 4, 1}}

SequencePosition[a, b, Overlaps -> All]

{{3, 5}, {5, 7}, {9, 11}}

and

SequenceCount[a, b, Overlaps -> All]

3

I have developed a deeper appreciation of Sequence* functions.

Answer 4

a = {1, 2, 3, 4, 6, 7, 2, 3, 4};
b = {2, 3, 4};
c = {2, 3, 4, 7};

Using SequenceSplit (new in 11.3)

sub[{a_, b_}] := MemberQ[b] @ SequenceSplit[a, x : b :> x]

sub /@ {{a, b}, {a, c}, {b, b}, {b, Reverse @ b}}

{True, False, True, False}

Answer 5

lst1={1,2,3,4,6,7};

lst2={2,3,4};

lst3={2,3,4,7};

---

Grabbing the @user1066's examples, my attempt is the following:

subListQ[a_, b_] := Module[{pos},
  pos = List@*Span @@@ MinMax /@ 
        Split[Position[a, Alternatives @@ b], #2[[1]] - #1[[1]] == 1 &];
  SameQ[DeleteCases[Extract[a, pos], b], {}]]
subListQ[lst1, lst2]
subListQ[lst1, lst3]
subListQ[lst1, lst1]
True
False
True

Testing subListQ with @eldo's examples:

a = {1, 2, 3, 4, 6, 7, 2, 3, 4};
b = {2, 3, 4};
c = {2, 3, 4, 7};
subListQ[#1, #2] & @@@ {{a, b}, {a, c}, {b, b}, {b, Reverse@b}}

{True, False, True, False}