Returning an InterpolatingFunction

Question

I am trying to write a function using Block that generates an InterpolatingFunction and then generates a second InterpolatingFunction that is a function of the first. I can return and use the first function but not the second. Below is a minimal version, with the negative sign standing in for a more general function. The result is that I can return values and plot f1 but not f2. How can one modify this to return a usable f2?

{f1, f2} = 
  Block[{dat1, dat2}, dat1 = ListInterpolation[{1, 2, 3, 4}];
   dat2 = -dat1;
   {dat1, dat2}];
{f1[1], f2[1]}
Plot[{f1[t], f2[t]}, {t, 1, 4}]

I just tried this, and that did not work, alas. (It returns -dat1[t] for f2[t].) — John Bechhoefer, Dec 07 '22 at 18:20
Thanks. This does work. An advantage of the Reinterpolation method below is that one ends up with a simpler InterpolatingFunction object that, for complicated functions, may be faster to evaluate. — John Bechhoefer, Dec 08 '22 at 21:02
Yes, perhaps less accurate. But in the particular application that motivated this post, I value speed of execution over accuracy (up to a point), so it might be a good tradeoff. — John Bechhoefer, Dec 09 '22 at 06:20
The reinterpolation is not smaller in the MWE, but it is when the interpolating function is cubic Hermite with derivative data at each node, such as produced by NDSolve[]. However, the reinterpolation is slower to evaluate than the cubic Hermite because a different algorithm is used. — Michael E2, Dec 09 '22 at 13:58
Please, what does "MWE" mean? In this case, the InterpolatingFunction is coming from a list (produced by FindRoot, but I don't think that changes anything). — John Bechhoefer, Dec 09 '22 at 15:57

score 3 · Answer 1 · answered Dec 07 '22 at 18:37

3

Try

{f1, f2} = Block[{dat1, dat2}, dat1 = ListInterpolation[{1, 2, 3, 4}];
dat2 = Apply[Function, { {u}, -dat1[u]}];
{dat1, dat2}];
{f1[1], f2[1]}(* {1,-1} *)
Plot[{f1[t], f2[t]}, {t, 1, 4}]

answered Dec 07 '22 at 18:37

Ulrich Neumann

53,729
2
23
55

Could you comment as to why this works when the original does not? I am not quite getting the issue. Also, I may have slightly oversimplified, as I would like to replace the minus sign function with an arbitrary function computed elsewhere. The following modification does not work:
```
myfunc[x_] := -x;
{f1, f2} = 
  Block[{dat1, dat2, t}, dat1 = ListInterpolation[{1, 2, 3, 4}];
   dat2 = Apply[Function, {{dat1}, myfunc[dat1]}];
   {dat1, dat2}];

Plot[{f1[t], f2[t]}, {t, 1, 4}]
```
– John Bechhoefer Dec 07 '22 at 18:53
Using dat2 = Apply[Function, {{t}, myfunc[dat1[t]]}]; instead works, so this does count as an answer to my question. Many thanks! Still, I'd be grateful to have a better understanding of what is going on. Why does it have to be {t} and not simply t, for example? – John Bechhoefer Dec 07 '22 at 19:26
1

Naming of the function argument t or u makes no difference! Apply is often useful in applying a function to an argument list. – Ulrich Neumann Dec 07 '22 at 21:18

Chris K · Accepted Answer · 2022-12-08T23:09:09.083

Based on this old question of mine, I wrote a function for this task in general, called Reinterpolate:

Reinterpolation::usage="Reinterpolation[f] reinterpolates a function containing one or more InterpolatingFunctions.";
Reinterpolation[f_,opts___?OptionQ]:=Module[{
(* options )
interpolationopts,interpolationpoints,
( other variables *)
xmin,xmax,ifs,grid,tmp},
(* handle options *)
interpolationopts=FilterRules[Flatten[{opts,Options[Reinterpolation]}],Options[Interpolation]];
interpolationpoints=Evaluate[InterpolationPoints/.Flatten[{opts,Options[Reinterpolation]}]];
ifs=Cases[f,_InterpolatingFunction,{0,[Infinity]}];
If[ifs=={},Return[f]];
If[interpolationpoints===Automatic,
    grid=Union[Flatten[Through[ifs["Grid"]],1]],
    {xmin,xmax}=ifs[[1,1,1]];
    grid=Table[x,{x,xmin,xmax,(xmax-xmin)/(interpolationpoints-1)}];
];
Quiet[
  tmp=Interpolation[Table[{Sequence@@val,f/.(if_InterpolatingFunction->if[Sequence@@val])},{val,grid}],Evaluate[Sequence@@interpolationopts]]
  ,{InterpolatingFunction::dmval}];
tmp[[1]]=ifs[[1,1]]; (* fix domain *)
Return[tmp]
];
Options[Reinterpolation]={InterpolationPoints->Automatic};

It works applied to your problem:

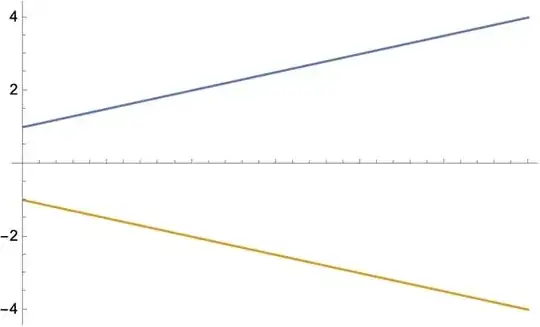
{f1, f2} = 
  Block[{dat1, dat2}, dat1 = ListInterpolation[{1, 2, 3, 4}];
   dat2 = Reinterpolation[-dat1];
   {dat1, dat2}];
{f1[1], f2[1]}
Plot[{f1[t], f2[t]}, {t, 1, 4}]
(* {1, -1} *)

I'd of course be interested in any improvements folks could suggest.

Addition 1:

OP @JohnBechhoefer asked whether this function could be modified to allow the explicit use of the independent variable. This seems to work already:

f1 = ListInterpolation[{1, 2, 3, 4}];
f2 = Reinterpolation[Piecewise[{{f1, t < 2.5}, {-f1, t >= 2.5}}]];
Plot[{f1[t], f2[t]}, {t, 1, 4}]

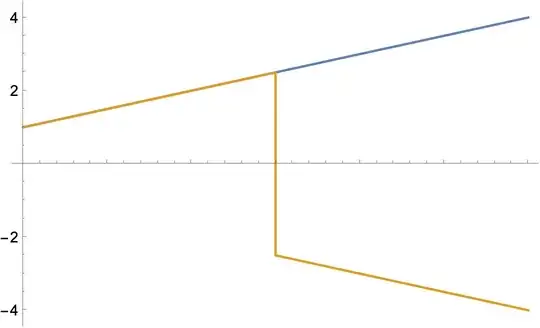
This was surprising, because I didn't try to build that functionality in. To see what's going on, we can look inside f2:

f2["ValuesOnGrid"]

An unintended happy side-effect! Is this sufficient for you? Otherwise it might be able to be calculated for each point in the new InterpolatingFunction if you have an example where this fails.

Thanks. Yes, it does work, but I think the simpler solution above will be enough. If I follow a bit what you are doing, it is choosing different points to base an interpolation on. I don't think that will be necessary in my application. (But we'll see....) — John Bechhoefer, Dec 07 '22 at 19:42
Yes, in my original application I wanted to transform the output of NDSolve, so I use the same points as in the original InterpolatingFunction. — Chris K, Dec 07 '22 at 19:58
As mentioned above, I realized that a point about your function is that it can condense a complicated function of an InterpolatingFunction into a single object, which should save time when subsequently using that function (in my case, as a "drive" in a system of ODEs in NDSolve). But one extension that would make it even more useful would be the ability to deal with Piecewise functions. This would require generalizing your routine to allow the "time" variable (implicit in my example) to appear explicitly. Have you thought about that case? — John Bechhoefer, Dec 08 '22 at 21:16
Thanks! But when I try this with this, with the original syntax, it does not work:
dat1 = ListInterpolation[{1, 2, 3, 4}]; dat2 = Reinterpolation[Piecewise[{{f1, t < 2.5}, {-f1, t >= 2.5}}]]; {dat1, dat2}]; Plot[{f1[t], f2[t]}, {t, 1, 4}]``` gives, for f2, just a line up to 2.5 and then nothing. [Sorry, I don't know how to include images and proper formatting in a comment.] — John Bechhoefer, Dec 09 '22 at 06:32
@JohnBechhoefer If you use it inside a Block, you need to use Global`t instead of t. — Chris K, Dec 09 '22 at 16:13

Returning an InterpolatingFunction

2 Answers2