0

I have an equation

$$ c \tan \left(\theta_{\mathrm{OPT}}\right)+\frac{a b A \exp \left(-b\left[\theta_{\mathrm{OPT}}-a\right]\right)}{\left[a \exp \left(-b\left[\theta_{\mathrm{OPT}}-a\right]\right)+1\right]^2}=0 $$

where a,b,c and A are constants. How can I solve this equation for $\theta_{OPT}$. Also is there any possibility to solve this equation in matlab/mathematica. I have tried taking natural log on both sides but it does not works.

I have tried the solve function in mathematica solve(((a b A exp(-b (x - a)))/(a exp(-b (x - a)) + 1)^2 = -c tan(x)),x)

noor
  • 3
  • 2
  • 1
    A numerical solution for given parameters isn't sufficient? – Ulrich Neumann Dec 13 '22 at 12:02
  • Welcome to the Mathematica Stack Exchange. Please share copy-paste-able Mathematica code for what you have tried so far. What are the constraints on the various constants? – Syed Dec 13 '22 at 12:18
  • Thanks, I have added mathematica pastable format above – noor Dec 13 '22 at 12:45
  • Maybe that is matlab syntax. You used solve instead of Solve and exp(-b (x - a)) instead of Exp[-b (x - a)]. Consider copy pasting the code from your Mathematica notebook. – userrandrand Dec 13 '22 at 15:13
  • It does not seem like Mathematica can solve that equation symbolically. Consider seperately the case c=0 and then divide by c and change A to w*c for example to absorb the c. That way you have one less parameter to consider when numerically solving the problem. That said you might want to revert to the previous coordinates after. For a graphical method of finding roots consider : https://mathematica.stackexchange.com/a/272002/86543. – userrandrand Dec 13 '22 at 15:47
  • @userrandrand If I use the original values will I be able to solve it. I mean instead of using symbolics use the actual values. – noor Dec 13 '22 at 16:11
  • Depends on the values. If all the values are 0 then probably. If Mathematica can not solve it symbolically then it is unlikely Mathematica will solve it for some random real number. This is different than Mathematica just taking very long to give an answer where yes a numerical rational value might give a result faster because Mathematica has to make less assumptions, There might be a subset of values where the equation is solvable. You might want to consider specifying the values you have in mind in your question – userrandrand Dec 13 '22 at 16:26
  • Consider also the following examples using ContourPlot to graphically find roots : https://mathematica.stackexchange.com/q/10807/86543 and https://mathematica.stackexchange.com/q/97937/86543 – userrandrand Dec 13 '22 at 16:45
  • @ userrandrand, Yes, I think this will be interesting. Thankyou! – noor Dec 13 '22 at 16:57
  • The @ should be next to the username like @noor or else the person will not be notified. I just happened to want to mention that sometimes there are analytical solutions for some integer values of parameters and sometimes also for rational values so you can also try such values if they provide insight (I did not try with this equation). Maybe with Trig functions replacing a parameter in the argument with Pi might also lead to some magical scenario where the equation is solvable – userrandrand Dec 13 '22 at 17:35

1 Answers1

1
expression = (a b A Exp[-b (x - a)])/(a Exp[-b (x - a)] + 1)^2 + 
  c Tan[x]

$$ \frac{a A b e^{-b (x-a)}}{\left(a e^{-b (x-a)}+1\right)^2}+c \tan (x) $$

Outline :

  • 1) Removing c from the parameters

  • 2) Finding some analytical solutions using FindInstance

  • 3) Using Manipulate and ContourPlot to find roots in an equation with many parameters

  • 4) Extracting the points from a given contour plot

  • 5) Polishing results with better accuracy

1) Removing c from the parameters

For non zero c, we can absorb the dependence on c by dividing by c and using A->c*w :

expression2 = expression/c /. A -> w*c // Simplify

$$\frac{a b w e^{b (x-a)}}{\left(e^{b (x-a)}+a\right)^2}+\tan (x)$$

That way there is one less parameter to consider but do not forget to check separately the case c=0. In the following I will focus on c non zero.

2) Finding some analytical solutions using FindInstance

For generic parameters Mathematica can not find a root for expression above. However, it can find instances of roots using FindInstance. For example, if we consider a to be positive then :

FindInstance[{expression2 == 0, a > 0}, {x, a, b, w}]

{{x->9392403/3312026,a->26566113/18118801,b->30971405/14149612,w->-((256374004055212 (26566113/18118801+E^(2545583876943569930325/849117367154967579512))^2 Tan[9392403/3312026])/(822789844998765 E^(2545583876943569930325/849117367154967579512)))}}

If you want a symbolic solution regardless of whether the solution is in terms of the variable x or one of the parameters, consider Solve or Reduce.

3) Using Manipulate and ContourPlot to find roots in an equation with many parameters

We can visualize dependence on parameters using (recall that c=0 should be considered separately):

Note: I chose the ranges of parameters in an arbitrary manner

  With[{expression2 = expression2}, 
 Manipulate[
  ContourPlot[expression2 == 0, {x, -4, 4}, {b, -4, 4}], {a, -4, 
   4}, {w, -4, 4}]]

enter image description here

4) Extracting the points from a given contour plot

If you want to extract the lines from a given value of a and w you can right click the plot and copy it and then paste into a new cell and use :

template of code below : points = Cases[Normal[... plot here ...], Line[x_] :> x, All]

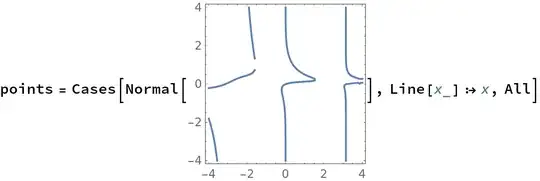
enter image description here

The points:

points // ListPlot

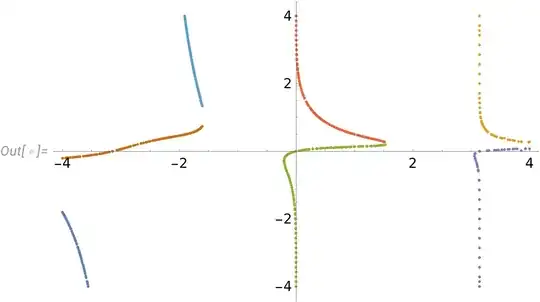
enter image description here

5) Polishing results with better accuracy

The points above might not be very accurate. In that case consider the numerical methods here: How to find seed values for solving nonlinear equations?

userrandrand
  • 5,847
  • 6
  • 33