Making a mesh from a set of points

Question

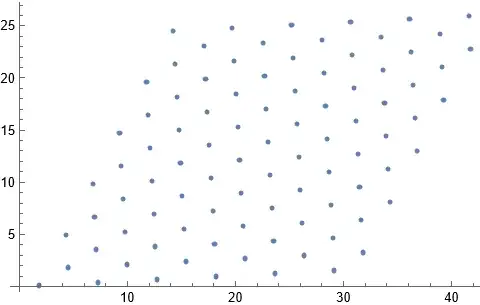
In conjunction with this question I find I am having difficulty making a mesh using a given set of points. The overarching objective is to make an interpolation function from an irregular set of points. I think the finite element method is the only one we have for doing this (am I correct here?). Here are the points and a plot of their locations:

 dd = {{14.2441`, 24.4802`}, {11.7597`, 19.6033`}, {14.4097`, 
        21.3246`}, {17.0598`, 23.0459`}, {19.7099`, 24.7671`}, {9.27522`, 
        14.7264`}, {11.9253`, 16.4477`}, {14.5754`, 18.1689`}, {17.2254`, 
        19.8902`}, {19.8755`, 21.6115`}, {22.5255`, 23.3327`}, {25.1756`, 
        25.054`}, {6.79079`, 9.84947`}, {9.44085`, 11.5707`}, {12.0909`, 
        13.292`}, {14.741`, 15.0133`}, {17.391`, 16.7345`}, {20.0411`, 
        18.4558`}, {22.6912`, 20.1771`}, {25.3412`, 21.8983`}, {27.9913`, 
        23.6196`}, {30.6414`, 25.3409`}, {4.30635`, 4.97255`}, {6.95642`, 
        6.69382`}, {9.60648`, 8.41508`}, {12.2565`, 10.1364`}, {14.9066`, 
        11.8576`}, {17.5567`, 13.5789`}, {20.2067`, 15.3002`}, {22.8568`, 
        17.0214`}, {25.5069`, 18.7427`}, {28.1569`, 20.464`}, {30.807`, 
        22.1852`}, {33.4571`, 23.9065`}, {36.1071`, 25.6278`}, {1.82192`, 
        0.095626`}, {4.47198`, 1.81689`}, {7.12205`, 3.53816`}, {9.77211`,
         5.25943`}, {12.4222`, 6.98069`}, {15.0722`, 8.70196`}, {17.7223`,
         10.4232`}, {20.3724`, 12.1445`}, {23.0224`, 13.8658`}, {25.6725`,
         15.587`}, {28.3226`, 17.3083`}, {30.9726`, 19.0296`}, {33.6227`, 
        20.7508`}, {36.2728`, 22.4721`}, {38.9228`, 24.1934`}, {41.5729`, 
        25.9146`}, {7.28768`, 0.382504`}, {9.93774`, 2.10377`}, {12.5878`,
         3.82504`}, {15.2379`, 5.54631`}, {17.8879`, 7.26757`}, {20.538`, 
        8.98884`}, {23.1881`, 10.7101`}, {25.8381`, 12.4314`}, {28.4882`, 
        14.1526`}, {31.1383`, 15.8739`}, {33.7883`, 17.5952`}, {36.4384`, 
        19.3164`}, {39.0884`, 21.0377`}, {41.7385`, 22.759`}, {12.7534`, 
        0.669382`}, {15.4035`, 2.39065`}, {18.0536`, 4.11192`}, {20.7036`,
         5.83318`}, {23.3537`, 7.55445`}, {26.0038`, 9.27572`}, {28.6538`,
         10.997`}, {31.3039`, 12.7183`}, {33.9539`, 14.4395`}, {36.604`, 
        16.1608`}, {39.2541`, 17.8821`}, {18.2192`, 0.95626`}, {20.8693`, 
        2.67753`}, {23.5193`, 4.39879`}, {26.1694`, 6.12006`}, {28.8194`, 
        7.84133`}, {31.4695`, 9.5626`}, {34.1196`, 11.2839`}, {36.7696`, 
        13.0051`}, {23.6849`, 1.24314`}, {26.335`, 2.9644`}, {28.9851`, 
        4.68567`}, {31.6351`, 6.40694`}, {34.2852`, 8.12821`}, {29.1507`, 
        1.53002`}, {31.8008`, 3.25128`}};
ListPlot[dd]

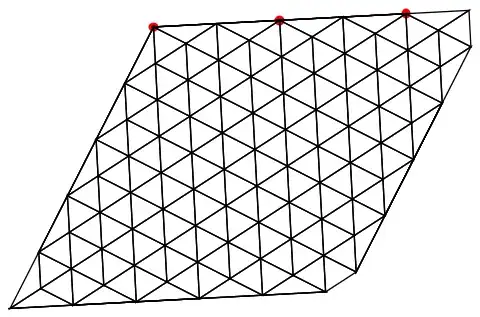
I have checked that there are no repeated points or points too close to each other. When I use the finite element method to make a mesh (as recommended here ) I get the following

Needs["NDSolve`FEM`"]
mesh = ToElementMesh[dd];
ToElementMesh::femimq: The element mesh has insufficient quality of 0.`. A quality estimate below 0. may be caused by a wrong ordering of element incidents or self-intersecting elements.

I can display the mesh and on examination of the quality I find there is one triangle that is poor quality

Show[mesh["Wireframe"]]
q = mesh["Quality"];
pos = Position[q, _?(# <= Min[q] &)];

The location of the bad triangle is along one edge, as can be seen from plotting the points of the triangle corners

badTriangles = Extract[ElementIncidents[mesh["MeshElements"]], pos];
pts = mesh["Coordinates"][[badTriangles[[1]]]];
Show[Graphics[{Red, PointSize[0.02], Point[pts]}], mesh["Wireframe"]]

It seems that the mesh generator is trying to make a triangle out of three points that lie along a straight line.

Is this a fault of the mesh generator? Is there a work around?

Thanks

The documented way to do this would be: ' mesh = ToElementMesh["Coordinates" -> dd];' However, that does not solve your problem. You could, as Ulrich explained, eliminate the bad triangle. In a future version (13.3) this is avoided by reordering the bad element. The will still have a poor quality element but it will have a positive quality measure. — user21, Dec 16 '22 at 15:04
@user21 I remembered the way you suggested here I guess that is being depreciated. — Hugh, Dec 16 '22 at 17:56
Yes, Hugh that's were this new syntax comes from. The other was never documented but I'll leave it in in order not to brake things. — user21, Dec 16 '22 at 19:06

score 2 · Answer 1 · answered Dec 16 '22 at 12:42

Workaround: Remove the elements with bad quality

Needs["NDSolve`FEM`"]
mesh = ToElementMesh[dd];
pts = mesh["Coordinates"];
triang = mesh["MeshElements"][[1, 1]];
quali = mesh["Quality"][[1]];
pos = Position[quali, _?(# > 10^-5 &)] // Flatten;
meshNew =ToElementMesh["Coordinates" -> pts,"MeshElements" ->{TriangleElement[triang[[pos]]]}]
Min[meshNew["Quality"]](* 0.599972 *)

Making a mesh from a set of points

1 Answers1

Linked