How to plot a cube using `ParametricPlot3D`?

Question

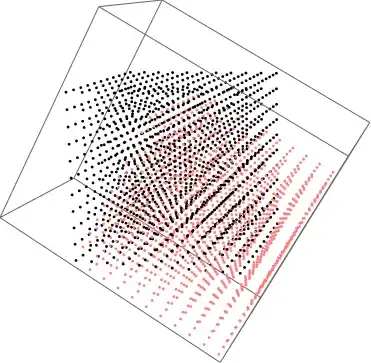
I have this code that plots a cube rotating around the z axes. I'm using a table of points and Graphics3D to visualize the motion. Is there a way to plot it using ParametricPlot3D?

delta = 0.1;
map[x_, theta_] := { x[[1]] Cos[theta] - x[[2]] Sin[theta], 
  x[[2]] Cos[theta] + x[[1]] Sin[theta], x[[3]]}
tab = Table[
   map[{x, y, z}, 0], {x, 0, 1, delta}, {y, 0, 1, delta}, {z, 0, 1, 
    delta}];
tab2 = Table[
   map[{x, y, z}, Pi/6], {x, 0, 1, delta}, {y, 0, 1, delta}, {z, 0, 1,
     delta}];
gp1 = Graphics3D[{Pink, 
    Table[Point[ Flatten[tab, 2][[i]]] , {i, 1, 
      Length[Flatten[tab, 2]]}]}];
gp2 = Graphics3D[{Black, 
    Table[Point[ Flatten[tab2, 2][[i]]] , {i, 1, 
      Length[Flatten[tab2, 2]]}]}];
Show[gp1, gp2]

Answer 1

Do you need it to be ParametricPlot3D? Here's another way to visualize using Graphics3D.

 grid3d = 
  Flatten[Join[
     Table[Line[{{a, b, -3}, {a, b, 3}}], {a, -3, 3}, {b, -3, 3}], 
     Table[Line[{{-3, a, b}, {3, a, b}}], {a, -3, 3}, {b, -3, 3}], 
     Table[Line[{{a, -3, b}, {a, 3, b}}], {a, -3, 3}, {b, -3, 
       3}]] 1];
Graphics3D[{FaceForm[{Opacity[0]}], grid3d}, Boxed -> False]