I would like to know the numerical value of a giant fraction, which I got from doing some combinatoric calculation (n choose k gets huge).
For example, say I have
Sum[Binomial[2048, k] (1/5)^k (4/5)^(2048 - k), {k, 9728/25, 10752/
25}]
This code runs fine and gives me a huge fraction, and I know its value should be somewhere between .6 and 1. However, I cannot simply use N[] or Round[] since the value gets too large/too small as Mathematica tries to work it out and reaches the precision limits of machine numbers.
What other options do I have for finding the value of this fraction?
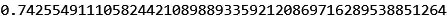




LeafCount /@ {sum, sum // Simplify}evaluates to{575, 295}– Bob Hanlon Dec 21 '22 at 05:54