Evaluate the following simple continued fractions

Question

A continued fraction is a fraction whose numerator is an integer and whose denominator is an integer added to a fraction whose numerator is an integer and whose denominator is an integer added to a fraction, and so on.

$$1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{...}}}}},$$

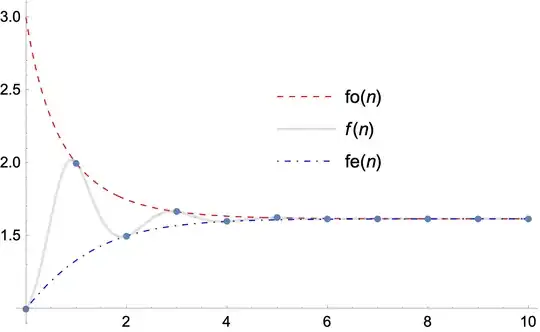
First, we will create a formula that expresses the above expression as a sequence. Second, we will calculate the first ten terms of the sequence that have created and represent it graphically. We will also try to calculate the 200th term of the sequence and finally, Finally, we will study the "connection" that continued fractions have with the quadratic equation.

We can write this "infinite fraction" as a sequence of terms, $t_n$, where

$t_0=1$
$t_1=1+1$
$t_2=1+\frac{1}{1+1}$
$t_3=1+\frac{1}{1+\frac{1}{1+1}}$
$\cdots$

So, if we determinate a generalized formula for $t_{n+1}$ in terms of $t_n$, we have the following formula $$t_{n+1}=1+\frac{1}{t_n}$$

Now, let's compute the decimal equivalents of the first 10 terms.

$t_0=1.000$
$t_1=1+1=2.000$
$t_2=1+\frac{1}{1+1}=1+\frac{1}{2}=\frac{3}{2}=1.500$
$t_3=1+\frac{1}{1+\frac{1}{1+1}}=1+\frac{1}{\frac{3}{2}}=1+\frac{2}{3}=\frac{5}{3}=1.666$
$t_4=1+\frac{1}{\frac{5}{3}}=1+\frac{3}{5}=\frac{8}{5}=1.600$
$t_5=1+\frac{1}{\frac{8}{5}}=1+\frac{5}{8}=\frac{13}{8}=1.625$
$t_6=1+\frac{1}{\frac{13}{8}}=1+\frac{8}{13}=\frac{21}{13}\simeq 1.615$
$t_7=1+\frac{1}{\frac{21}{13}}=1+\frac{13}{21}=\frac{34}{21}\simeq 1.619$
$t_8=1+\frac{1}{\frac{34}{21}}=1+\frac{21}{34}=\frac{55}{34}\simeq 1.618$
$t_9=1+\frac{1}{\frac{55}{34}}=1+\frac{34}{55}=\frac{89}{55}\simeq 1.618$
$t_{10}=1+\frac{1}{\frac{89}{55}}=1+\frac{55}{89}=\frac{144}{89}\simeq 1.618$

   fromTerms[terms_List] := Fold[#2 + 1/#1 &, Reverse@terms]
        set = {1, 2, 3, 4, 5};
        fromTerms[set];
        FromContinuedFraction[set];
        proceduralFromTerms[terms_List] := 
         Module[{frac = terms[[-1]]}, 
          Do[frac = terms[[i]] + 1/frac, {i, -2, -Length[terms], -1}];
          frac]
          fromTerms[Array[x, 10]]

My question is the following: how could I use the code above to calculate the first ten terms and then plot them?

seems related : https://mathematica.stackexchange.com/a/22018/86543 — userrandrand, Dec 21 '22 at 16:03
But to answer the question, the built in way is x[1] + Table[ContinuedFractionK[x[i], {i, 2, b}], {b, 2, 10}] /. x -> (1 &) (you can remove the replacement rule if you want a symbollic expression) — userrandrand, Dec 21 '22 at 16:21
Also, maybe, SubstitutionSystem[{n_-> 1+ 1/n}, {1}, 10]//Flatten — user1066, Oct 17 '23 at 22:27

score 4 · Answer 1 · answered Dec 21 '22 at 11:43

NestList[1 + 1/# &, 1, 10]

{1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89}

To visualize (a few terms shown):

NestList[1 + 1/Defer@# &, 1, 10]

% //. Defer[x_] :> x

{1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89}

Bob Hanlon · Accepted Answer · 2022-12-21T18:15:58.353

$Version

(* "13.2.0 for Mac OS X x86 (64-bit) (November 18, 2022)" *)

Clear["Global`*"]

Use RSolve

f[n_] = t[n] /. RSolve[{t[n] == 1 + 1/t[n - 1], t[0] == 1}, t[n], n][[1]] // 
  Simplify
(* 1 + Fibonacci[n]/Fibonacci[1 + n] *)
f[n] // FunctionExpand // FullSimplify
(* (2 (2 + Sqrt[5]) (3 + Sqrt[5])^n - 
 2^n (-1 + Sqrt[5]) Cos[n π])/((3 + Sqrt[5])^(1 + n) + 
 2^(1 + n) Cos[n π]) *)
f[200]
(* 734544867157818093234908902110449296423351/

453973694165307953197296969697410619233826 *)
% // N[#, 20] &
(* 1.6180339887498948482 *)
Limit[f[n], n -> Infinity]
(* 1/2 (1 + Sqrt[5]) *)
Show[
 Plot[f[n], {n, 0, 20}, PlotRange -> All],
 DiscretePlot[f[n], {n, 0, 20}]]

Numerically,

FixedPoint[1 + 1.0/# &, 1] // RootApproximant
(* 1/2 (1 + Sqrt[5]) *)

EDIT: Adding the upper and lower bounds

For n even

fe[n_] = FullSimplify[f[n] // FunctionExpand, Mod[n, 2] == 0]
(* 1 + ((1 + Sqrt[5]) (-4^n + (1 + Sqrt[5])^(2 n)))/(
 2^(1 + 2 n) + (1 + Sqrt[5])^(2 n) (3 + Sqrt[5])) *)

For n odd

fo[n_] = FullSimplify[f[n] // FunctionExpand, Mod[n, 2] == 1]
(* 1 + ((1 + Sqrt[5]) (4^n + (1 + Sqrt[5])^(2 n)))/(-2^(
   1 + 2 n) + (1 + Sqrt[5])^(2 n) (3 + Sqrt[5])) *)
Legended[
 Show[
  Plot[Evaluate[
    Tooltip /@ {fo[n], f[n], fe[n]}],
   {n, 0, 10},
   PlotStyle -> {
     {Red, Dashed, AbsoluteThickness[0.75]},
     Opacity[0.25, Gray],
     {Blue, DotDashed, AbsoluteThickness[0.75]}},
   PlotRange -> All],
  DiscretePlot[f[n], {n, 0, 10}, Filling -> None]],
 Placed[
  LineLegend[{
    {Red, Dashed, AbsoluteThickness[0.75]},
    Opacity[0.25, Gray],
    {Blue, DotDashed, AbsoluteThickness[0.75]}},
   {HoldForm@fo[n], HoldForm@f[n], HoldForm@fe[n]}],
  {.6, .6}]]

Oh thanks! I found the same plot but I like yours better – Athanasios Paraskevopoulos Dec 21 '22 at 17:51 — Athanasios Paraskevopoulos, Dec 21 '22 at 17:51

score 2 · Answer 3 · answered Dec 21 '22 at 11:37

You already calculated the first 10 terms. Do you want a shorter code? Anyway, you can get the terms by recursion, like:

Clear[t]
t[0] = 1;
t[n_] := 1 + 1/t[n - 1];
terms = Table[t[n], {n, 0, 10}]
(* {1, 2, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89} *)

Or in decimal notation:

terms // N
(*{1., 2., 1.5, 1.66667, 1.6, 1.625, 1.61538, 1.61905, 1.61765, \
1.61818, 1.61798} *)

score 2 · Answer 4 · answered Dec 21 '22 at 11:44

You can use NestList to obtain the sequence. You only need to definea function that maps from previous to the next term in the sequence.

f=1+1/# &
NestList[f,1,10]//N
(*
{1., 2., 1.5, 1.6666666666666667, 1.6, 1.625, 1.6153846153846154, 
 1.619047619047619, 1.6176470588235294, 1.6181818181818182, 
 1.6179775280898876}
*)

BTW, this sequence has a fixed point which also happens to be the limit $\ell=\frac{1+\sqrt{5}}{2}$

Evaluate the following simple continued fractions

4 Answers4