Why, if you write the expression in the form of two functions, does the code stop working?

Question

I would like to find the minimum of the function EER[a, v] using parallel computing.

If I write the code like this, it works:

ClearAll["Global`*"]
Kx[a_?NumericQ] := 
  NIntegrate[(E^(-((2 r)/a)) (-2 a + r))/(
    a^2 r NIntegrate[Exp[-(r/a)]^2 r^2, {r, 0, [Infinity]}])*
    r^2, {r, 0, [Infinity]}];
Ko[v_?NumericQ] := ((-1.05 + 0.69* v)* v)/(2.27 + v (-3.02 + 1.1 v));
EER[a_, v_] := Ko[v]*Kx[a];
Exx = 
 ParallelTable[{v, 
   FindMinimum[{Etmp = EER[a, v], (0.1 < a < 30)}, {{a, 1}}, 
    EvaluationMonitor :> {Pause[0.1], 
      Print[" Current a=", a, " E=", Etmp]}]}, {v, {7.5, 10, 12.5, 
    15}}]

Now I want to denote part of the expression in Kx[a_?NumericQ] like K[a_?NumericQ] but in the case of such entry, the code stops working. Why doesn't the code work?

ClearAll["Global`*"]
K[a_?NumericQ] := (E^(-((2 r)/a)) (-2 a + r))/(
 a^2 r NIntegrate[Exp[-(r/a)]^2 r^2, {r, 0, [Infinity]}])
Kx[a_?NumericQ] := NIntegrate[K[a]*r^2, {r, 0, [Infinity]}];
Ko[v_?NumericQ] := ((-1.05 + 0.69* v)* v)/(2.27 + v (-3.02 + 1.1 v));
EER[a_, v_] := Ko[v]*Kx[a];
Exx = 
 ParallelTable[{v, 
   FindMinimum[{Etmp = EER[a, v], (0.1 < a < 30)}, {{a, 1}}, 
    EvaluationMonitor :> {Pause[0.1], 
      Print[" Current a=", a, " E=", Etmp]}]}, {v, {7.5, 10, 12.5, 
    15}}]

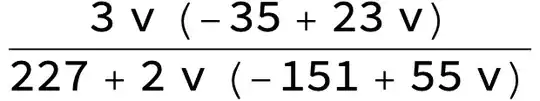
Short answer: Do not use K, rename to K2 for example. Longer answer: K is a built-in symbol, in particular Context[K] is System`. This means that the definition you have given for K is not automatically distributed to other kernels, only definitions for symbols in Global` are. — user293787, Dec 21 '22 at 19:24
use small k, always in Mathematica avoid using capitals, because they are mostly reserved for predefined functions — nufaie, Dec 21 '22 at 20:25
The list of capital letters that are built in https://mathematica.stackexchange.com/q/117877/86543 — userrandrand, Dec 21 '22 at 21:52

score 0 · Answer 1 · answered Dec 21 '22 at 23:53

Clear["Global`*"]

Your functions can be evaluated symbolically

Kx[a_] = Integrate[(E^(-((2 r)/a)) (-2 a + r))/
    (a^2 r Integrate[Exp[-(r/a)]^2 r^2, {r, 0, ∞}])*
   r^2, {r, 0, ∞}]

Ko[v_] =
 ((-1.05 + 0.69*v)*v)/(2.27 + v*(-3.02 + 1.1*v)) //
   Rationalize // FullSimplify

EER[a_, v_] = Ko[v]*Kx[a]

min[v_] = MinValue[{EER[a, v] // Normal,
   1/10 <= a <= 30}, a]

arg[v_] := ArgMin[{EER[a, v] // Normal,
   1/10 <= a <= 30}, a]
Off[ArgMin::wksol]
Show[
 Plot3D[EER[a, v], {v, 15/2, 15}, {a, 1/10, 1},
  AxesLabel -> (Style[#, 14] & /@ {v, a, EER}),
  ClippingStyle -> None,
  PlotRange -> All],
 Graphics3D[{Red, AbsolutePointSize[4],
   Point[{#, arg[#], min[#]} & /@
     Range[15/2, 15, 1/2]]}]]

Prepend[
  N@{#, arg[#], min[#]} & /@ Range[15/2, 15, 1/2],
  {v, a, "E"}] // Grid[#, Frame -> All] &

Why, if you write the expression in the form of two functions, does the code stop working?

1 Answers1