0

I am attempting to see the contour plot for the function, Sqrt[y-x]==z. The graph shows an odd structure that seems to fall where a vertical asymptote would exist. What can I do to eliminate the odd structure? Here is my code for it:

ContourPlot3D[Sqrt[y-x]==z,{x,-6,6},{y,0,6},{z,0,4}]

and here is the result:

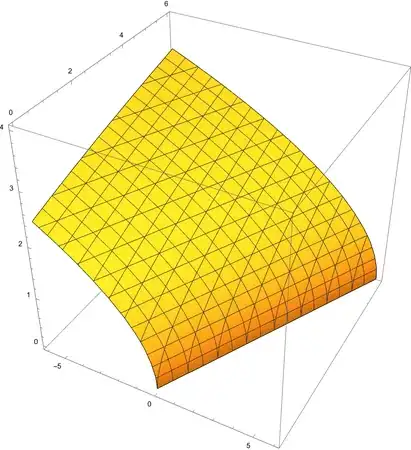
enter image description here

GeorgeE
  • 47
  • 3
  • 3
    ContourPlot3D[Re[Sqrt[y - x]] == z, {x, -6, 6}, {y, 0, 6}, {z, 0, 4}, AxesLabel -> Automatic] – Bob Hanlon Dec 22 '22 at 15:34
  • Thanks Bob. I am fairly new to Mathematica. I knew there was a real number issue just by what was going on in the graph. I was unaware that adding the Re would only allow real number output. This helps tremendously. – GeorgeE Dec 22 '22 at 16:41
  • 1
    @BobHanlon ContourPlot3D[Re[Sqrt[y - x]] == z, {x, -6, 6}, {y, 0, 6}, {z, -4, 4}, AxesLabel -> Automatic] will get the wrong result. The result contain a part of z==0 and y<=x. – cvgmt Dec 23 '22 at 01:42

1 Answers1

4

It is a bug.

we have to remove Sqrt from the original equation.

ContourPlot3D[y - x == z^2, {x, -6, 6}, {y, 0, 6}, {z, 0, 4}]

Or

ContourPlot3D[y - x == z^2, {x, -6, 6}, {y, 0, 6}, {z, -4, 4}, 
 RegionFunction -> Function[{x, y, z}, z >= 0], 
 RegionBoundaryStyle -> None]

enter image description here

Or use ImplicitRegion, still avoid Sqrt.

reg = ImplicitRegion[{y - x == z^2, 
   z >= 0}, {{x, -6, 6}, {y, 0, 6}, {z, -4, 4}}]
RegionPlot3D[DiscretizeRegion@reg, Axes -> True, BoxRatios -> 1, 
 Mesh -> 10]

enter image description here

cvgmt
  • 72,231
  • 4
  • 75
  • 133