I need to generate regularly spaced samples (points) from the surface of unit simplexes with 2 or greater vertices or end points.
I can generate random samples pretty straightforwardly:
sampleSimplex[sampleSize_, vertices_] :=
Module[{s},
s = RandomReal[ExponentialDistribution[2], {sampleSize, vertices}];
Map[Normalize[#, Total] &, s]]
Graphics3D[Point /@ sampleSimplex[1000, 3], ImageSize -> 150,
BoxStyle -> Directive[LightGray], ViewPoint -> {Pi, Pi/2, 2}]

This works nicely and enables me to specify the number of samples and the number of vertices, but as I stated above I want to generate regularly spaced points, kind of like a Mesh on a 3D plot (but not limited to 3 dimensions).
I can also do it for 2 vertices pretty simply:
sampleSimplexWith2Vertices[sampleSize_] := Module[{temp},
temp = N[Range[0, 1, 1/sampleSize]];
Transpose[{temp, Reverse[temp]}]]
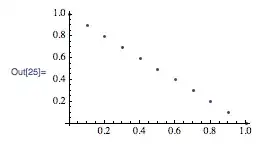
sampleSimplexWith2Vertices[10]
{{0., 1.}, {0.1, 0.9}, {0.2, 0.8}, {0.3, 0.7}, {0.4, 0.6}, {0.5,
0.5}, {0.6, 0.4}, {0.7, 0.3}, {0.8, 0.2}, {0.9, 0.1}, {1., 0.}}
ListPlot[%, ImageSize -> 200]
but I seem blocked in thinking about a solution that extends further.
Any suggestions for how to approach this problem appreciated.
I recognize that this may appear too narrow in scope or that it seems more like a conceptual problem of how to think about the problem more than how to implement an idea in Mathematica. I can withdrawal the question, if either of those seems like the consensus.
I hoped that the approaches I've tried so far and those the question might draw would have sufficient general interest to merit some responses.
In the interest of improving the question I wanted to incorporate @Rahul_Narain's idea from his comment:
sampleSimplexWith3Vertices[pointsPerSide_] := N@Select[
Flatten[
Table[{x, y, 1 - x - y}, {x, 0, 1, 1/pointsPerSide}, {y, 0, 1,
1/pointsPerSide}], 1], #[[3]] >= 0 &]
sampleSimplexWith3Vertices[10];

This works for 3 vertices, where one specifies the number of points per side. But, how does one generalize this for an arbitrary number of vertices (dimensions)? I've thought that Table would give one way to go about this, but wouldn't generalizing this with Table need a way to change just about everything between its brackets?
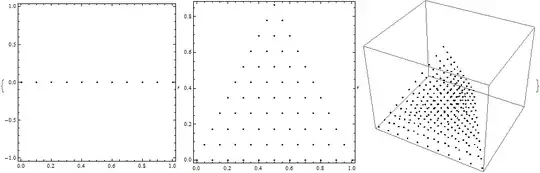
p = Select[Flatten[Table[{x, y, 1 - x - y}, {x, 0, 1, 1/n}, {y, 0, 1, 1/n}], 1], #[[3]] >= 0 &]I am not adept enough with Mathematica to write a general-purpose function for arbitrary dimensions, so I will leave that for someone else to answer. – Jun 27 '13 at 15:32