Here's how I approach singular solutions. I sometimes have to think about a step somewhere in the middle, so it's not quite an algorithm yet. I think of an ODE $F(x,y(x),y'(x))=0$ as a manifold $F(x,y,p)=0$ in 3-space on which there is a vector field, called the contact field, corresponding to $p=dy/dx$: The "slope" of a solution curve as viewed from above is given by the height $p$ of the surface. (The solution or integral curve is the parametric curve $(x,y,p)=(x,y(x),y'(x))$.)
There are two sorts of singularities: Those in the manifold itself (such as self-intersections), and those where the field is undefined, which happens when $\partial F/\partial p = 0$.
DSolve also adds solutions, under IncludeSingularSolutions, that are limits of the general solution at boundaries of the domain of the integration parameter (usually C[1]). In fact it seems to check only infinity and zero and does not look into whether there are other boundaries in the domain of C[1].
Since we're looking at examples of DSolve, we can construct mesh functions that show the solution curves on the ODE manifold, which I wanted to share.
Example 1
ode = x^2*(y'[x])^2 - y[x]^2 == 0;
manifold = ode /. {y'[x] -> p, y[x] -> y};
Reduce[{manifold, D[manifold, p]}, {x, y, p}] (* sing sols *)
dsol = DSolve[ode, y, x, IncludeSingularSolutions -> True]
(*ode/.dsol//Simplify*) (* check dsol *)
{mfns, mesh} = dsol // solToMeshFunction // Transpose
ContourPlot3D[manifold // Evaluate,
{x, -1, 1}, {y, -1, 1.01}, {p, -5.01, 5},
AxesLabel -> Automatic,
MeshFunctions -> mfns // Evaluate,
Mesh -> mesh /. Automatic -> 15 // Evaluate,
MeshShading -> RandomColor[RGBColor[_, _, _, 0.5], {4, 4, 2}]]
(*
* A sing. pt. (not sol.) and sing. sol. y == 0
(x == 0 && y == 0) || (y == 0 && p == 0)
{{y -> Function[{x}, C[1]/x]},
{y -> Function[{x}, x C[1]]},
{y -> Function[{x}, 0]}}
{{Function[{x, y, p}, -p x^2], Function[{x, y, p}, p],
Function[{x, y, p}, p - 0]}, (* redundent b/c sol is redundant )
{Automatic, Automatic, {0}}}
)
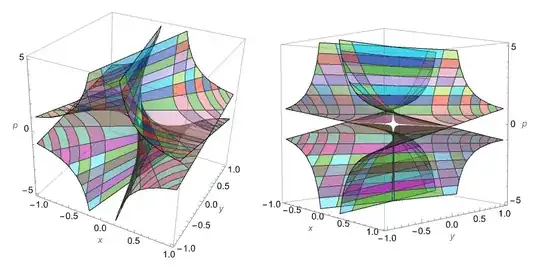
The tartan grid is formed by the two families of solutions,
the hyperbolas and lines. The line y == 0 is a singular locus
of the manifold that happens to be a solution to the ODE,
as well as a particular value of the general solution.
Example 2
ode = x*(y'[x])^2 - (2*x + 3*y[x])*y'[x] + 6*y[x] == 0;
manifold = ode /. {y'[x] -> p, y[x] -> y};
Reduce[{manifold, D[manifold, p]}, {x, y, p}] (* sing sols *)
dsol = DSolve[ode, y, x, IncludeSingularSolutions -> True]
(*ode/.dsol//Simplify*)
{mfns, mesh} = dsol // solToMeshFunction // Transpose
ContourPlot3D[manifold // Evaluate,
{x, -1, 1}, {y, -1, 1.01}, {p, -3.01, 7},
AxesLabel -> Automatic,
MeshFunctions -> mfns // Evaluate,
Mesh -> mesh /. Automatic -> 15 // Evaluate,
MeshShading -> RandomColor[RGBColor[_, _, _, 0.5], {4, 4, 2}],
ViewPoint -> {20, 0, 0}, ViewVertical -> {0, 0, 1}]
(*
* A sing. pt. (not a sol.) and sing. locus (not a sol.)
(x == 0 && y == 0) ||
(y == (2 x)/3 && p == 2) || (* y == 2x/3 is split into two cases *)
(y == (2 x)/3 && x != 0 && p == 2)
{{y -> Function[{x}, x^3 C[1]]},
{y -> Function[{x}, 2 x + C[1]]},
{y -> Function[{x}, 0]}} (* spurious *)
{{Function[{x, y, p}, p/(3 x^2)], Function[{x, y, p}, -2 x + y],
Function[{x, y, p}, p - 0]}, {Automatic, Automatic, {0}}}
*)
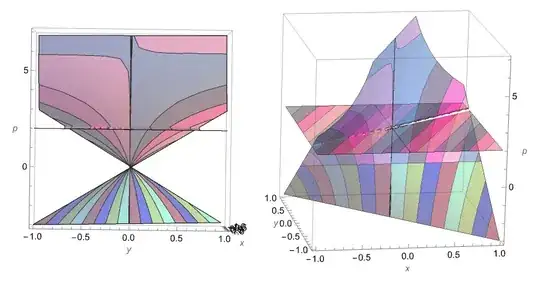
The line y == 0 is not a singular locus
of the manifold, just the point at the origin.
It happens to be a solution to the ODE,
in fact a particular value of the general solution,
and perhaps that's why it was retained in the output of DSolve[].
As can be seen, y == 2x/3, which shows up in Reduce[]
output, is a self-intersection of the manifold. It is at
a height of p == 2 and would have to have slope 2
to be a solution. So it's not a singular solution.
Example 3
This is a classic Clairaut equation.
ode = y[x] == y'[x]*x + 1/y'[x];
manifold = ode /. {y'[x] -> p, y[x] -> y};
Reduce[{manifold, D[manifold, p]}, {x, y, p}] (* sing sols *)
dsol = Cases[DSolve[ode, y, x, IncludeSingularSolutions -> True],
s_ /; FreeQ[s, Indeterminate]]
(*ode/.dsol//Simplify*)
{mfns, mesh} = dsol // solToMeshFunction // Transpose
Show[
ContourPlot3D[p y == 1 + p^2 x, {x, -5, 5.01},
{y, -5, 5.007}, {p, -10.01, 10},
AxesLabel -> Automatic, MaxRecursion -> 3,
PlotPoints -> {15, 45, 45},
MeshFunctions -> mfns // Evaluate,
Mesh -> mesh /. Automatic ->
Subdivide[-(9.5^(1/3)), (9.5^(1/3)), 25]^3 //
Evaluate,
MeshShading -> RandomColor[RGBColor[_, _, _, 0.5], {4, 2, 2}]]]
(*
* Two singular solutions (or one if y^2 == 4x)
(y == -2 Sqrt[x] || y == 2 Sqrt[x]) && x != 0 && p == y/(2 x)
{{y -> Function[{x}, 1/C[1] + x C[1]]},
{y -> Function[{x}, -2 Sqrt[x]]},
{y -> Function[{x}, 2 Sqrt[x]]}}
{{Function[{x, y, p}, p],
Function[{x, y, p}, p - -(1/Sqrt[Max[1.*10^-16, x]])],
Function[{x, y, p},
p - 1/Sqrt[Max[1.*10^-16, x]]]}, {Automatic, {0}, {0}}}
*)
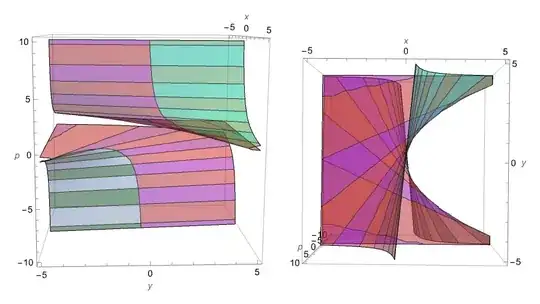
The top view shows that the tangent planes are vertical along the singular solutions. This is equivalent to $\partial F/\partial p = 0$. See DSolve misses a solution of a differential equation for a more
in-depth analysis of a similar singular solution.
solToMeshFunctions
solToMeshFunction // ClearAll;
solToMeshFunction::dim = "Dimension of solution ``, expected 1.";
solToMeshFunction::fo = "First-order ODEs only (no systems).";
solToMeshFunction[sols_ : {__List}] :=
Flatten[solToMeshFunction /@ sols, 1];
solToMeshFunction[{sol_Rule}] := solToMeshFunction[sol];
solToMeshFunction[{_Rule, __Rule}] := Null /; (
Message[solToMeshFunction::fo]; False);
solToMeshFunction[sol : (y_[x_] -> _)] :=
solToMeshFunction[DSolve`DSolveToPureFunction[sol]];
solToMeshFunction[sol : (y_ -> Verbatim[Function][{x_}, s_])] /;
FreeQ[sol, _C] :=
With[{yp = y'[x] /. sol /.
Power[b_, r_] /; EvenQ[Denominator@r] :>
Power[Max[10.^-16, b], r]},
{{Function @@ Hold[{x, y, p}, p - yp], {0}}}
];
solToMeshFunction[sol : (y_ -> Verbatim[Function][{x_}, s_])] :=
With[{param = DeleteDuplicates@Cases[s, _C, Infinity]},
If[Length@param != 1,
Message[solToMeshFunction::dim, Length@param]
];
With[{mf = First@param /. Replace[
Solve[p == (y'[x] /. sol), param],
{} :> Solve[y == s, param]
] /.
Power[b_, r_] /; EvenQ[Denominator@r] :>
Power[Max[10.^-16, b], r]},
{Function @@ Hold[{x, y, p}, #], Automatic} & /@ mf
] /; Length@param == 1
];
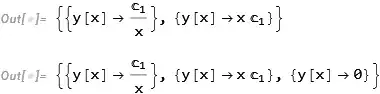
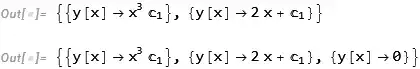


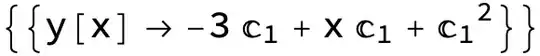



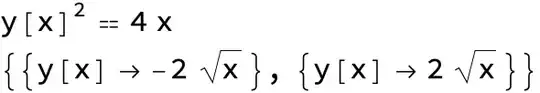








yto zero in the ODE and see if there are constant solutions to the resulting algebraic equation. These do not seem to be checked against special values of the general solution. (This is how they[x] -> 0solutions are added to the solution set.) SeePrintDefinitions@DSolve`DSolveSingularSolutionsfor code. – Michael E2 Jan 16 '23 at 17:53C[1]approaches 0, ±∞. These are usually not, strictly speaking, "singular solutions" (at least not of the form found in your Clairaut equation). – Michael E2 Jan 16 '23 at 18:00