2

I am trying to understand this code

ClearAll["Global`*"]

CoefficientRules[13r^2 - 7r + 2, r];


f[a_, n_] := a^2 + n;


Map[Function[{x}, f[165/100, x[[1, 1]] + 1]x[[2]]], 
 CoefficientRules[13r^2 - 7*r + 2, r]]

I don't understand this part f[165/100, x[[1, 1]] + 1]*x[[2]] , could you please explain this notation and if it's possible to rewrite this line in a less abbreviated version?

Mam Mam
  • 1,843
  • 2
  • 9
  • 1
    Hold[< unknown expression >] // FullForm will expand the short forms enough to point you to the documentation. – Bob Hanlon Dec 25 '22 at 21:41

1 Answers1

5

Maybe this makes it little more clear

ClearAll["Global`*"]
f[a_, n_] := a^2 + n;
coeff = CoefficientRules[56*r^4 + 13*r^2 - 7*r + 2, r]
g[x_] := f[165/100, x[[1, 1]] + 1]*x[[2]];
(g[#] &) /@ coeff

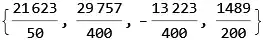
Mathematica graphics

Could you rewrite this part ((g[#] &) /@ coeff) without #, & and /@

One way might be

Table[ g[coeff[[n]]], {n, 1, Length@coeff}]

Mathematica graphics

Or

 First@Last@Reap@Do[ Sow@g[coeff[[n]]], {n, 1, Length@coeff}]

Mathematica graphics

But whatever you do, do not use For.

But using Map (which is what &/@ does it better and shorter.

Adding Lukas suggestion also:

 Map[g, coeff]

Mathematica graphics

Update

And I don't understand this line g[x_] := f[165/100, x[[1, 1]] + 1]*x[[2]], the argument x is a matrix 2X2?

x in this context is each entry of coeff. But coeff is

coeff = CoefficientRules[56*r^4 + 13*r^2 - 7*r + 2, r]

Mathematica graphics

So when you do Map, each x will be one entry in the above list. i.e. {4} -> 56 then {2} -> 13 then {1} -> -7 and so on until all entries are used in the list. So x is each one of these. Let look at one of them

({4} -> 56)[[1, 1]]

Mathematica graphics

({4} -> 56)[[2]]

Mathematica graphics

Now you see what f[165/100, x[[1, 1]] + 1]*x[[2]] does. For this entry, it becomes f[165/100, 4+1]*56

Nasser
  • 143,286
  • 11
  • 154
  • 359