Finding numerically roots of equation over region

Question

I'm trying to solve the following numerical problem:

I have a function of 2 variables in some rectangular region, the function is computed numerically with some moderate time cost (solution of linear differential equation with those variables as parameters, though it is not important here).

Let's assume here without loss of generality that the function is

f[x_,y_] = (Sin[x] Sin[5 y]/y - 0.3)^2 for 0<x<Pi/2, -2<y<2

I'm trying to obtain efficient numerically (heavy cost of calling function) and transparent way to finding 2d curves for which this function is 0.

To exemplify, I can obtain such curves by calling ContourPlot

ContourPlot[f[x,y], {x, 0, Pi/2}, {y, -2, 2}, ContourShading -> None, Contours -> {0.01}]

Mind that for every minimum reaching 0 there are 2 lines because I had to use nonzero contour value, and also because of precision some contours aren't fully found.

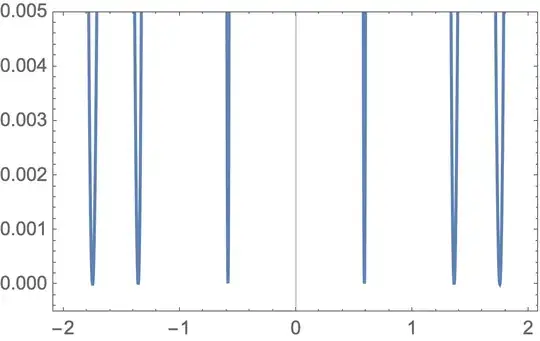
Taking specific choice for this example, let's say I want on some sections find y = g[x], which I tried to do by finding zeros for slice of function f for given x.

In other words I have plot like this for some given x

And I want to find all zeros.

In theory it should be easy, but I had problems using with NMinimize and FindRoot (although maybe solution lies with them). Solution like this (namely reintegrating function) is out of question due to high computational cost.

When in given slice there are multiple roots, I assume I will be able to classify them by hand (as in this example), but I need a method to find them all or find specific one that is continuous across different slices.

score 1 · Answer 1 · answered Dec 28 '22 at 22:07

If there are potential precision issues, Rationalize all constants so that you can use arbitrary precision rather than machine precision.

f[x_, y_] = (Sin[x] Sin[5 y]/y - 0.3)^2 // Rationalize
(* (-(3/10) + (Sin[x] Sin[5 y])/y)^2 *)

The cross-section of f[1, y] in the vicinity of the roots

plt = Plot[f[1, y], {y, -2, 2},
  PlotRange -> {-.0005, .005},
  Frame -> True]

Use the plot to select starting values for FindRoot

roots = FindRoot[f[1, y] == 0, {y, #},
    WorkingPrecision -> 15] & /@
  {-1.75`15, -1.35`15, -0.6`15, 0.6`15, 1.35`15, 1.75`15}
(* {{y -> -1.75019152453211}, {y -> -1.35769057873158}, {y -> 

-0.586209238653224}, {y -> 0.586209238653224}, {y -> 1.35769057873158}, {y -> 
   1.75019152453211}} *)

Checking,

f[1, y] /. roots
(* {9.18353310^-15, 2.28361110^-14, 3.65955410^-14, 3.65955410^-14, 
 2.28361110^-14, 9.18353310^-15} *)

Thanks for answer, that's working solution for slice, but: first - this is a toy model and the function in actual calculations is numerical second: the manual part of finding roots for one slice is ok, however in the end a function y[x] for each root is needed (continuous through multiple slices) — NightsBlackBird, Dec 28 '22 at 22:26

score 1 · Answer 2 · answered May 28 '23 at 03:00

A common way to get a numerical function is to use NDSolve to integrate the derivative obtained from implicit differentiation.

f[x_, y_] = (Sin[x] Sin[5 y]/y - 0.3)^2;
ics = Solve[Rationalize@f[1, y] == 0 && -2 < y < 2, y, 
    GeneratedParameters -> c] // DeleteDuplicates;
ode = y'[x] == Simplify@ First@
    SolveValues[D[Rationalize@f[x, y[x]] == 0, x], y'[x]];
ysols = Flatten@Values[
    Table[
     Quiet[
      NDSolve[
       {ode,
        y[1] == (y /. ic)},
       y, {x, 0, Pi},
       Method -> "ExplicitRungeKutta",(* or Automatic, etc. )
       "ExtrapolationHandler" -> {Indeterminate &, 
         "WarningMessage" -> False},
       WorkingPrecision -> MachinePrecision
       ],
      ( NDSolve will stop when it gets to the end of the
       * curve and issue a warning (stiffness/zero step size)
       * which we suppress  *)
      {NDSolve::ndstf, NDSolve::ndsz}],
     {ic, ics}]];
Plot[Evaluate@Through[ysols[x]], {x, 0, Pi}]

Note: Use WorkingPrecision -> $MachinePrecision or higher to keep extrapolation from leaking. Extrapolation can cause spikes at the ends of the graphs since the derivative is very large. You might ask why does extrapolation leak? I supposed it has to do with comparison machine-precision floats with tolerance, but setting Internal`$EqualTolerance = 0, Internal`$SameQTolerance = 0 does not solve it. And the tolerance is quite large.

Finding numerically roots of equation over region

2 Answers2