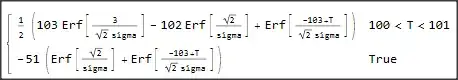I had thought that with the following two integrals, I was simply expressing the same idea in two different but equivalent ways, with the range of the values (excluding x) within the Floor[] term being, in both instances, in the interval [100,101). Nonetheless, they produce inconsistent results. In the first integral, the sum 100+T is in the interval [100,101) because of the assumptions about T :
Integrate[
(Floor[100 + T + x])*PDF[NormalDistribution[0, sigma], x], {x, 2, 3},
Assumptions -> {T \[Element] Reals, sigma \[Element] Reals,
sigma > 0, 0 <= T < 1}]
whereas in this second integral, T itself is in the interval [100,101)
Integrate[
(Floor[T + x])*PDF[NormalDistribution[0, sigma], x], {x, 2, 3},
Assumptions -> {T \[Element] Reals, sigma \[Element] Reals,
sigma > 0, 100 <= T < 101}]
Have I done something wrong or misunderstood something, or am I just being blind to an elementary mistake?