Crossposted: https://community.wolfram.com/groups/-/m/t/2763509
I'd like to classify rational numbers on a unit circle by the following property: number of digits in the denominator. It relates to an article I read:
https://www.quantamagazine.org/secret-link-uncovered-between-pure-math-and-physics-20171201
I built a function for the search, but it runs terribly slow - any ideas on speeding this up are highly appreciated:
ClearAll[ratUni];
ratUni[n_Integer]:=
(filter out on rational numbers)
Cases[
(find counterpart Pythagorean coordinate on unit square)
Map[Sqrt[1-#^2]&,
(also remove fractions that simplify to less-than-n digits in denominator)
Parallelize@Select[
(*build all fractions with denominators and numerators of exactly n digits and remove duplicates*)
Union[Divide@@@Flatten[Table[{m,k},{k,Range[10^n-1]},{m,k-1}],1]],
Length[IntegerDigits[Denominator[#]]]>n-1&]],
_Rational]
Simplest example of rational numbers on unit circle with denominator of 1 digit:
In[]:= ratUni[1]
Out[]= {4/5, 3/5}
Works fine for rational numbers on unit circle with denominator of 2 digits:
In[]:= ratUni[2]
% // Length
Out[]= {84/85, 60/61, 40/41, 63/65, 24/25, 35/37, 12/13, 77/85,
80/89, 15/17, 56/65, 45/53, 55/73, 72/97, 21/29, 20/29, 65/97, 48/73, 28/53, 33/65, 8/17, 39/89, 36/85, 5/13, 12/37, 7/25, 16/65, 9/41, 11/61, 13/85}
Out[]= 30
Still OK for 3 digits but already takes 7 seconds to compute:
In[]:= ratUni[3] // Length // AbsoluteTiming
Out[]= {6.47679, 284}
For 4 digits it is a disastrous 1237 seconds and for 5 digits it hangs. Any help on optimizing it is highly appreciated.
In[]:= ratUni[4] // Length // AbsoluteTiming
Out[]= {1237.74, 2870}

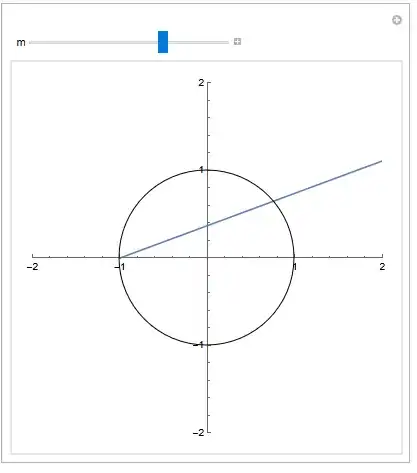

{-R,0}(where $R$ is the circle radius), and the line has a rational slope $m$ (which you can set to anything). You intersect the line with with the circle and you get coordinates of rational Pythagorean triples which you can then multiply up to get integer solutions. No need for optimization, brute force, or searching. – flinty Jan 06 '23 at 19:56{x,y}={(1 - m^2)/(1 + m^2), (2 m)/(1 + m^2)}and since you picked a rational $m$, they are all rational pythag triples. - No need for sqrt or anything like that. – flinty Jan 06 '23 at 20:05