Unstable boundary values using NDSolve?

Question

I have an equation:

w1[u_]=-(1/2) u^2 ea e0 Sin[2 a[z]] + K (a''[z])

with numerical values,

K = 6.2*10^-12; ea = 10; e0 = 8.85*10^-12; L = 1;
nd=NDSolve[{w1[1]==0,a[0]==0,a[L]==0},a[z],{z,0,L}];
gr1 = Plot[a[z] /. nd[[1]], {z, 0, L}, PlotRange -> Automatic]

The NDSolve should give the following output for different u, for u equal to zero a is 90 and by increasing u, a decreases till 0. Boundary conditions: @ z=0 and L a is 0 (very known problem),

However, the NDSolve is unstable and not giving the exact solution for the above program. Any suggestions or recommendations.

Two comments: ele is undefined and is bad practice to use specific capital letters with K being one of them; see here — bmf, Jan 10 '23 at 13:10
Well, I doubt that NDSolve is making an error, This tells me you have something wrong with your ode or with some of the numerical values you are using. Are you sure you are using same ode and parameter values used to generate the plot you are showing? — Nasser, Jan 10 '23 at 13:23
Complementary to what @Nasser wrote is it possible that for u=0 we have a[0] == 90, a[L] == 90. Also, can you be more specific in this part and by increasing u, a decreases till 0? — bmf, Jan 10 '23 at 13:25
@Nasser a link to paper (https://www.sciencedirect.com/science/article/pii/S0301679X17303092), I am trying to replicate, page 3 equation 4 and figure 3. — a019, Jan 10 '23 at 13:26
@MuhammadAli perhaps you should provide a link to the pdf or better yet add the details to the OP. — bmf, Jan 10 '23 at 13:28
@bmf https://reader.elsevier.com/reader/sd/pii/S0301679X17303092?token=72A12685951CE9177FA3BD9A77CBB9AFB905AE5182027B39B216BD59F8865847564C998967FCFA7268AB685732C2033A&originRegion=eu-west-1&originCreation=20230110132930 — a019, Jan 10 '23 at 13:29
I had quick look at the paper. Notice it says for fig 4, it is using the normalized z* which is z/h (do not know what h is. Planck's constant?) and your U is E*h. I think the problem is scaling/normalization issue as the ode look OK. May be if you use the normalized values, the plot will show OK since h=6.62607015 × 10-34 which will make big difference in scaling. — Nasser, Jan 10 '23 at 13:40
@Naseer Normalize z means here is that diving by the thickness, so z* goes 0 to 1. h is thickness, what I wrote is fine, I am having the same problem with Mathematica for quite some time. — a019, Jan 10 '23 at 13:44

Alex Trounev · Accepted Answer · 2023-01-28T14:14:30.030

6

This problem can be solved with using the Euler wavelets collocation method described in our paper, we have

w1[u_] = -u^2 Sin[2 a[z]]/kk/2 + (a''[z]); ea = 10; e0 = 
 8.85*10^-12; kk = 6.2*10^-12/ea/e0; L = 1;
UE[m_, t_] := EulerE[m, t];
psi[k_, n_, m_, t_] := 
  Piecewise[{{2^(k/2) UE[m, 2^k t - 2 n + 1], (n - 1)/2^(k - 1) <= t <
       n/2^(k - 1)}, {0, True}}];
PsiE[k_, M_, t_] := 
 Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 3; M0 = 7; With[{k = k0, M = M0}, 
 nn = Length[Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]];
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; zcol = 
 xcol = Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, nn + 1}]; Psijk = 
 With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 = 
 With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1];
Psi[y_] := Psijk /. t1 -> y; int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y; A = Array[as, {nn}];
X2[y_] := A . Psi[y]; X1[y_] = A . int1[y] + c1; 
X0[y_] = A . int2[y] + c1 y + c2; eq = 
 Table[-(1/2) u^2 Sin[2 X0[y]]/kk + X2[y] == 0, {y, 
   xcol}]; bc = {X0[0] == Pi/2, X0[1] == Pi/2};
var = Join[A, {c1, c2}]; Do[
 soln[j] = 
   FindRoot[Join[eq, bc] /. u -> j, 
    Table[{var[[i]], 1/10}, {i, Length[var]}]];, {j, 0, 7}]
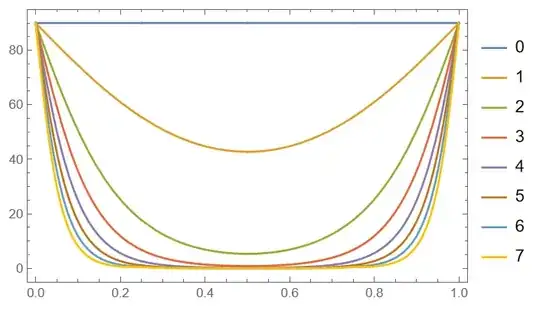
Plot[Evaluate[Table[2 90 /Pi X0[y] /. soln[j], {j, 0, 7}]], {y, 0, 1},
  Frame -> True, PlotLegends -> Table[j, {j, 0, 7}]]

edited Jan 28 '23 at 14:14

answered Jan 10 '23 at 15:50

Alex Trounev

44,369
3
48
106

1

wonderful stuff! – bmf Jan 10 '23 at 15:52
@AlexTrounev Can the same method be extended to similar solution but more complex problem such as for two coupled equations and four boundary conditions? The end solution is similar but starting from 2 and stabilizing at 90. I am trying NDSolve , shooting method but after certain range the NDSolve with shooting method can not find the solution. eq1: w1[u_]= L/K3(1/4 ((2−3 ) Sin[4 [z]] '[z]^2+2 Sin[2 [z]] (e0 ea '[z]^2+(3−1 ) '[z]^2+2 '[z]^2 ))+(1 Cos[[z]]^2+3 Sin[[z]] ) (d'[z])/d)=0. – a019 Jan 26 '23 at 15:17
@Alex Trounev eq2. w2= L/K3(Cos[[z]](−2(2+(2−3 ) Cos[2 [z]] Sin[[z]] '[z] '[z]+Cos[[z]](2 Cos[[z]]^2+3 Sin[[z]]^2) (d'[z])/d))=0. The parameters are now, K1=13.410^-12, K2=610^-12, K3=18.510^-12, ea=11.35, e0=8.8510^-12, L=1. Boundary conditions, [0]== [L]==2*(Pi/180), [0]==0, [L]==Pi/2. And u goes again from 0,to 7. The end solution is similar but starting from 2 and stabilizing at 90. Kind of mirror image of the above. Instead of a[z], now there is [z] and [z] and {z,0,L}. Extension of the same problem. – a019 Jan 26 '23 at 15:20
@MuhammadAli Yes, it can be extended to solve more complicated problem. – Alex Trounev Jan 27 '23 at 04:26
@AlexTrounev I am not getting the same output, the one you showed above. Is there anything to do with the version of Mathematica I am using (11.0). I am adding a link to the https://imgur.com/a/6ijQjDU I tried with different things and plotrange but still not. – a019 Jan 27 '23 at 08:41
@MuhammadAli Did you use code from my answer? – Alex Trounev Jan 28 '23 at 05:56
@AlexTrounev Yes, I copied and paste, and got a different output (https://imgur.com/a/6ijQjDU). That's why I am a bit surprised whether it is do with the Mathematica version or not? – a019 Jan 28 '23 at 07:42
@MuhammadAli It looks like there was some typo in the code, let try the updated one. – Alex Trounev Jan 28 '23 at 09:58
@AlexTrounev still not, now the code gives errors when we execute the var... command "Findroots: error: is not a list of numbers". I think you replaced k0 with k – a019 Jan 28 '23 at 14:06
@MuhammadAli I see that we have two definitions for k0. Try new code with kk instead of k0. – Alex Trounev Jan 28 '23 at 14:16
@AlexTrounev Thanks! it works now, I'll try to expand the method for a more complicated problem (very known though) the one which I mentioned above!! – a019 Jan 28 '23 at 15:36

Unstable boundary values using NDSolve?

1 Answers1

Linked