2

I'm using NDSolve to simulate the following model of phase separation: enter image description here

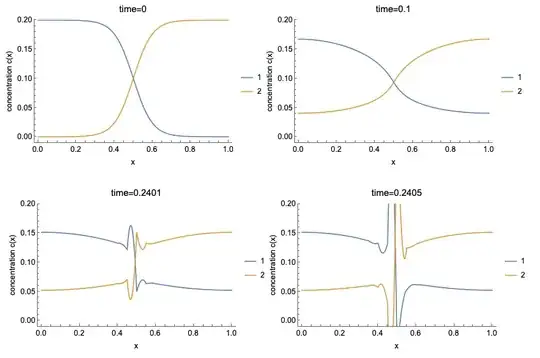
where rho_T=rho_1+rho_2. The term with chi causes rho_1 and rho_2 to repel each other. However, there is a numerical instability at the interface which causes the solution to blow up: enter image description here

Refining the mesh narrows the cusps, but they still diverge and cause the integration to halt. How can I use NDSolve to solve this system?

Here is the code in Mathematica 13.1. Note that decreasing chi allows NDSolve to converge, but you end up with a uniform solution instead of two domains.

rhoT = rho1[t, x] + rho2[t, x];

chi = 10.5;


vars = {{rho1[t, x], rho2[t, x]}, t, {x}};
op = D[vars[[1]], t] + 
   DiffusionPDETerm[
    vars, {{alpha1/rhoT, 
      alpha1(rho1[t, x]/rhoT)chi}, {alpha2(rho2[t, x]/rhoT)chi, 
      alpha2/rhoT}}];


(no-flux boundary conditions)


bcConserved = NeumannValue[0, x == 0] + NeumannValue[0, x == l];


alpha1 = 1;
alpha2 = 1;


tF = 1;
e0 = 0.1;
l = 1;


(initial conditions)


f1[x_] := (e0/
     l)(20/(Log[20(1 + E^(10l))] - Log[20(1 + E^(-10l))]))/(1 + 
      E^(20(x - l/2)));


f2[x_] := (e0/
     l)(-(20/(Log[20E^(10l) (1 + E^(10l))] - 
           Log[20(1 + E^(10l))]))/(1 + E^(20*(x - l/2))) + 2);


ic1 = rho1[0, x] == f1[x];


ic2 = rho2[0, x] == f2[x];


sol = NDSolveValue[{op == {bcConserved, bcConserved}, ic1, 
    ic2}, {rho1, rho2}, {t, 0, tF}, {x, 0, l}];


{r1, r2} = sol;


Plot[{r1[tF, x], r2[tF, x]}, {x, 0, l}, PlotLegends -> {"1", "2"}, 
 PlotRange -> {Automatic, Full}, LabelStyle -> Directive[Black, 10]]
ben.w
  • 43
  • 5
  • This is a typical problem with pure Neumann boundary conditions discussed on https://mathematica.stackexchange.com/questions/191476/poisson-equation-with-pure-neumann-boundary-conditions/191518#191518 – Alex Trounev Jan 13 '23 at 04:33
  • @AlexTrounev, how do get to this conclusion? This is a time dependent problem, while the one you link to is a stationary problem. – user21 Jan 13 '23 at 05:52
  • The second equation is independent from the first, is that right? Where does this equation come from? – user21 Jan 13 '23 at 05:57
  • @user21 There is a typo in the Latex form equation for $\rho_2$. Equations should be symmetrical. But in the code there is the symmetry. – Alex Trounev Jan 13 '23 at 06:48
  • @user21 Alex Trounev is correct about the typo, and I have updated the question accordingly. This is certainly time-dependent though. These equations come from a model of diffusion where the flux J=-alphacgrad(mu), where mu is the chemical potential: mu_i = ln(rho_i)+ chi *rho_j.

    I will take a look at the post Alex Trounev shared, although it will take some time to understand.

     – ben.w Jan 13 '23 at 16:08
  • @ben.w thanks. Where does this eqn come from? A book, paper, did you conceive it? – user21 Jan 13 '23 at 16:11
  • 1
    @user21 It's a mass-transfer equation where rho is the mass density and the flux J=-alpha * concentration * gradient of chemical potential. The concentration is rho/rhoT. The chemical potential is mu_i =ln(rho_i)+chi * rho_j. (I'm playing fast and loose with units here, but that's not the source of the problem.)

    It's very similar to Eq. 10 in this paper, although I'm working on a slightly different problem. https://pubs.rsc.org/en/content/articlelanding/2019/sm/c8sm02045k

     – ben.w Jan 13 '23 at 16:37
  • @ben.w See also https://mathematica.stackexchange.com/questions/202446/solving-cahn-hilliard-equation-linearsolve-linear-equation-encountered-that-ha – Alex Trounev Jan 14 '23 at 06:52

0 Answers0