3

Hi all (probably Jose),

I am not sure if I am misunderstanding some fundamental GR topic or if I am using the package wrong. I would at some point like to contract over the components of the metric tensor which should involve expanding covariant derivatives into Christoffels then into derivatives of the metric (c.f. my last question). I then assume that I would need to have my elements expressed in a specific basis, say cartesian for ease. So, the way I call elements changes from u[-a] to u[{-a,-cartesian}].

So, I'm a little confused though when I take the covariant derivative of an arbitrary vector and depending on using or not using a basis get different answers. Consider the following:

Clear["Global`*"]
<< xAct`xCoba`
$PrePrint = ScreenDollarIndices
DefManifold[M,4,{a,b,c,d,e,f,i,j,k,m,n,p,q,r,s}]
DefBasis[cartesian, TangentM, {0,1,2,3}]
DefTensor[u[-a],M]
CovDToChristoffel[PDcartesian[-a][u[b]]]
CovDToChristoffel[PDcartesian[{-a,-cartesian}][u[b]]]
CovDToChristoffel[PDcartesian[-a][u[{b,cartesian}]]]
CovDToChristoffel[PDcartesian[{-a,-cartesian}][u[{b,cartesian}]]]

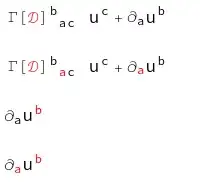
Which gives me 4 output lines of: enter image description here

Beyond the color coding to indicate a basis, I don't think I understand why the Christoffels are vanishing in the last two examples. Appologies if this is a fundamental geometry question I'm missing.

user64494
  • 26,149
  • 4
  • 27
  • 56
akozi
  • 853
  • 3
  • 10

1 Answers1

3

The notation u[{a, B}] in xCoba means the product u[b] Basis[-b, {a, B}], which is a scalar. A vector field is an object with a free abstract index. Basis indices like {a, B} do not count. Therefore u[a] is a vector field, but u[{a, B}] is a scalar field in xCoba. All covariant derivatives of scalar fields coincide, so there is no need to add Christoffel terms when changing from your PDcartesian to PD.

Similarly, PD[{-a, -cartesian}][...] is equivalent to the product Basis[{-a, -cartesian}, b] PD[-b][...].

You may find more standard to use the alternative notation TensorDerivative[u, PD][a, -b] instead of PD[-b][u[a]]. Now TensorDerivative[u, PD] is a tensor with two abstract indices (note the differentiation index is placed last), and you can take components as TensorDerivative[u, PD][{a, B}, {-b, -B}] without the basis vectors being differentiated.

akozi
  • 853
  • 3
  • 10
jose
  • 6,328
  • 1
  • 14
  • 24
  • 1
    Ahhh, got it! I think I was under the impression that the notation of {a,B} was for eventually indicating what the abstract indexes needed to be summed over in the future by way of a chart. Like indicating that Cartesian would index over x, y, z, t for instance.

    It seems obvious now but I kind of assumed that the basis in the notation was basically book keeping until an eventual contraction over the indices. Whereas, this is much more literal in how I should think about it. Thanks Jose! :)

     – akozi Jan 18 '23 at 22:00