Separating two peaks in a 2D array of data

Question

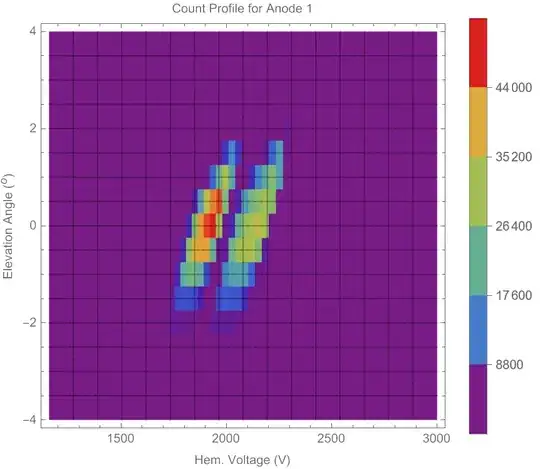
I have a 2D array of count values and the data presents two peaks separated by a valley of low counts. I want to be able to separate each peak signal from the other so that I can analyse the behaviour of these peaks individually.

I have included an example data set at the end of this message (apologies for its length I wasn't sure how to create a smaller artificial data set that had the same features).

Plotting this data in a ListDensityPlot gives the following figure:

My first thought was to convert this array in to an array of 0's and 1's; counts above a certain threshold are set to 1 and counts below threshold are set to 0. I have been able to do this like so:

newData = {};
func[t_] := Flatten[Table[If[data[[i, 3]] < t, Append[newData, 0], Append[newData, 1]], {i, 1, Length[data], 1}]]

Plotting this function yields the following plot:

I think that the next step would be to isolate each peak and then multiply the original data set by the separated arrays of 0's and 1's to isolate each peak in the original array.

This last step is where I am stuck. I would really appreciate if somebody could help me here.

Thanks.

data={{3000., -4., 0}, {2955., -4., 0}, {2910.68, -4., 0}, {2867.01, -4., 
  0}, {2824.01, -4., 0}, {2781.65, -4., 0}, {2739.92, -4., 
  0}, {2698.83, -4., 0}, {2658.34, -4., 0}, {2618.47, -4., 
  0}, {2579.19, -4., 0}, {2540.5, -4., 0}, {2502.4, -4., 
  0}, {2464.86, -4., 0}, {2427.89, -4., 0}, {2391.47, -4., 
  0}, {2355.6, -4., 0}, {2320.26, -4., 0}, {2285.46, -4., 
  0}, {2251.18, -4., 0}, {2217.41, -4., 0}, {2184.15, -4., 
  3}, {2151.39, -4., 3}, {2119.12, -4., 2}, {2087.33, -4., 
  8}, {2056.02, -4., 16}, {2025.18, -4., 10}, {1994.8, -4., 
  9}, {1964.88, -4., 1}, {1935.41, -4., 1}, {1906.37, -4., 
  0}, {1877.78, -4., 0}, {1849.61, -4., 0}, {1821.87, -4., 
  0}, {1794.54, -4., 0}, {1767.62, -4., 0}, {1741.11, -4., 
  0}, {1714.99, -4., 0}, {1689.27, -4., 0}, {1663.93, -4., 
  0}, {1638.97, -4., 0}, {1614.38, -4., 0}, {1590.17, -4., 
  1}, {1566.32, -4., 0}, {1542.82, -4., 0}, {1519.68, -4., 
  0}, {1496.88, -4., 0}, {1474.43, -4., 0}, {1452.31, -4., 
  1}, {1430.53, -4., 0}, {1409.07, -4., 0}, {1387.93, -4., 
  0}, {1367.12, -4., 0}, {1346.61, -4., 0}, {1326.41, -4., 
  1}, {1306.51, -4., 0}, {1286.92, -4., 0}, {1267.61, -4., 
  0}, {1248.6, -4., 0}, {1229.87, -4., 1}, {1211.42, -4., 
  0}, {1193.25, -4., 0}, {1175.35, -4., 0}, {1157.72, -4., 
  0}, {3000., -3.5, 0}, {2955., -3.5, 0}, {2910.68, -3.5, 
  0}, {2867.01, -3.5, 0}, {2824.01, -3.5, 0}, {2781.65, -3.5, 
  0}, {2739.92, -3.5, 0}, {2698.83, -3.5, 0}, {2658.34, -3.5, 
  0}, {2618.47, -3.5, 0}, {2579.19, -3.5, 0}, {2540.5, -3.5, 
  0}, {2502.4, -3.5, 0}, {2464.86, -3.5, 0}, {2427.89, -3.5, 
  0}, {2391.47, -3.5, 0}, {2355.6, -3.5, 0}, {2320.26, -3.5, 
  0}, {2285.46, -3.5, 0}, {2251.18, -3.5, 0}, {2217.41, -3.5, 
  0}, {2184.15, -3.5, 4}, {2151.39, -3.5, 4}, {2119.12, -3.5, 
  6}, {2087.33, -3.5, 13}, {2056.02, -3.5, 19}, {2025.18, -3.5, 
  16}, {1994.8, -3.5, 20}, {1964.88, -3.5, 10}, {1935.41, -3.5, 
  10}, {1906.37, -3.5, 4}, {1877.78, -3.5, 0}, {1849.61, -3.5, 
  1}, {1821.87, -3.5, 0}, {1794.54, -3.5, 1}, {1767.62, -3.5, 
  1}, {1741.11, -3.5, 0}, {1714.99, -3.5, 1}, {1689.27, -3.5, 
  0}, {1663.93, -3.5, 0}, {1638.97, -3.5, 0}, {1614.38, -3.5, 
  1}, {1590.17, -3.5, 0}, {1566.32, -3.5, 0}, {1542.82, -3.5, 
  0}, {1519.68, -3.5, 0}, {1496.88, -3.5, 0}, {1474.43, -3.5, 
  0}, {1452.31, -3.5, 0}, {1430.53, -3.5, 0}, {1409.07, -3.5, 
  0}, {1387.93, -3.5, 0}, {1367.12, -3.5, 0}, {1346.61, -3.5, 
  1}, {1326.41, -3.5, 0}, {1306.51, -3.5, 0}, {1286.92, -3.5, 
  0}, {1267.61, -3.5, 1}, {1248.6, -3.5, 0}, {1229.87, -3.5, 
  0}, {1211.42, -3.5, 0}, {1193.25, -3.5, 0}, {1175.35, -3.5, 
  0}, {1157.72, -3.5, 0}, {3000., -3., 0}, {2955., -3., 
  0}, {2910.68, -3., 0}, {2867.01, -3., 0}, {2824.01, -3., 
  0}, {2781.65, -3., 0}, {2739.92, -3., 0}, {2698.83, -3., 
  0}, {2658.34, -3., 0}, {2618.47, -3., 0}, {2579.19, -3., 
  0}, {2540.5, -3., 0}, {2502.4, -3., 0}, {2464.86, -3., 
  0}, {2427.89, -3., 0}, {2391.47, -3., 0}, {2355.6, -3., 
  0}, {2320.26, -3., 0}, {2285.46, -3., 0}, {2251.18, -3., 
  0}, {2217.41, -3., 0}, {2184.15, -3., 4}, {2151.39, -3., 
  14}, {2119.12, -3., 17}, {2087.33, -3., 37}, {2056.02, -3., 
  47}, {2025.18, -3., 62}, {1994.8, -3., 45}, {1964.88, -3., 
  42}, {1935.41, -3., 14}, {1906.37, -3., 8}, {1877.78, -3., 
  0}, {1849.61, -3., 1}, {1821.87, -3., 2}, {1794.54, -3., 
  0}, {1767.62, -3., 0}, {1741.11, -3., 0}, {1714.99, -3., 
  0}, {1689.27, -3., 0}, {1663.93, -3., 0}, {1638.97, -3., 
  0}, {1614.38, -3., 0}, {1590.17, -3., 1}, {1566.32, -3., 
  0}, {1542.82, -3., 0}, {1519.68, -3., 1}, {1496.88, -3., 
  1}, {1474.43, -3., 0}, {1452.31, -3., 0}, {1430.53, -3., 
  0}, {1409.07, -3., 0}, {1387.93, -3., 2}, {1367.12, -3., 
  0}, {1346.61, -3., 0}, {1326.41, -3., 0}, {1306.51, -3., 
  0}, {1286.92, -3., 0}, {1267.61, -3., 0}, {1248.6, -3., 
  0}, {1229.87, -3., 0}, {1211.42, -3., 0}, {1193.25, -3., 
  0}, {1175.35, -3., 0}, {1157.72, -3., 0}, {3000., -2.5, 
  0}, {2955., -2.5, 0}, {2910.68, -2.5, 0}, {2867.01, -2.5, 
  0}, {2824.01, -2.5, 0}, {2781.65, -2.5, 0}, {2739.92, -2.5, 
  0}, {2698.83, -2.5, 0}, {2658.34, -2.5, 0}, {2618.47, -2.5, 
  0}, {2579.19, -2.5, 0}, {2540.5, -2.5, 0}, {2502.4, -2.5, 
  0}, {2464.86, -2.5, 0}, {2427.89, -2.5, 0}, {2391.47, -2.5, 
  0}, {2355.6, -2.5, 0}, {2320.26, -2.5, 0}, {2285.46, -2.5, 
  0}, {2251.18, -2.5, 0}, {2217.41, -2.5, 3}, {2184.15, -2.5, 
  6}, {2151.39, -2.5, 26}, {2119.12, -2.5, 60}, {2087.33, -2.5, 
  88}, {2056.02, -2.5, 137}, {2025.18, -2.5, 162}, {1994.8, -2.5, 
  153}, {1964.88, -2.5, 82}, {1935.41, -2.5, 45}, {1906.37, -2.5, 
  14}, {1877.78, -2.5, 2}, {1849.61, -2.5, 0}, {1821.87, -2.5, 
  2}, {1794.54, -2.5, 0}, {1767.62, -2.5, 1}, {1741.11, -2.5, 
  2}, {1714.99, -2.5, 0}, {1689.27, -2.5, 0}, {1663.93, -2.5, 
  1}, {1638.97, -2.5, 1}, {1614.38, -2.5, 0}, {1590.17, -2.5, 
  0}, {1566.32, -2.5, 0}, {1542.82, -2.5, 1}, {1519.68, -2.5, 
  3}, {1496.88, -2.5, 0}, {1474.43, -2.5, 0}, {1452.31, -2.5, 
  2}, {1430.53, -2.5, 0}, {1409.07, -2.5, 0}, {1387.93, -2.5, 
  1}, {1367.12, -2.5, 0}, {1346.61, -2.5, 1}, {1326.41, -2.5, 
  0}, {1306.51, -2.5, 0}, {1286.92, -2.5, 0}, {1267.61, -2.5, 
  0}, {1248.6, -2.5, 0}, {1229.87, -2.5, 0}, {1211.42, -2.5, 
  0}, {1193.25, -2.5, 0}, {1175.35, -2.5, 1}, {1157.72, -2.5, 
  0}, {3000., -2., 0}, {2955., -2., 0}, {2910.68, -2., 
  0}, {2867.01, -2., 0}, {2824.01, -2., 0}, {2781.65, -2., 
  0}, {2739.92, -2., 0}, {2698.83, -2., 0}, {2658.34, -2., 
  0}, {2618.47, -2., 0}, {2579.19, -2., 0}, {2540.5, -2., 
  0}, {2502.4, -2., 0}, {2464.86, -2., 0}, {2427.89, -2., 
  0}, {2391.47, -2., 0}, {2355.6, -2., 0}, {2320.26, -2., 
  0}, {2285.46, -2., 0}, {2251.18, -2., 0}, {2217.41, -2., 
  2}, {2184.15, -2., 23}, {2151.39, -2., 53}, {2119.12, -2., 
  169}, {2087.33, -2., 348}, {2056.02, -2., 704}, {2025.18, -2., 
  1582}, {1994.8, -2., 1656}, {1964.88, -2., 1574}, {1935.41, -2., 
  1506}, {1906.37, -2., 26}, {1877.78, -2., 10}, {1849.61, -2., 
  247}, {1821.87, -2., 952}, {1794.54, -2., 1099}, {1767.62, -2., 
  1168}, {1741.11, -2., 1342}, {1714.99, -2., 403}, {1689.27, -2., 
  16}, {1663.93, -2., 13}, {1638.97, -2., 0}, {1614.38, -2., 
  3}, {1590.17, -2., 2}, {1566.32, -2., 2}, {1542.82, -2., 
  0}, {1519.68, -2., 1}, {1496.88, -2., 1}, {1474.43, -2., 
  1}, {1452.31, -2., 3}, {1430.53, -2., 4}, {1409.07, -2., 
  3}, {1387.93, -2., 0}, {1367.12, -2., 0}, {1346.61, -2., 
  0}, {1326.41, -2., 0}, {1306.51, -2., 2}, {1286.92, -2., 
  0}, {1267.61, -2., 1}, {1248.6, -2., 1}, {1229.87, -2., 
  2}, {1211.42, -2., 0}, {1193.25, -2., 1}, {1175.35, -2., 
  1}, {1157.72, -2., 0}, {3000., -1.5, 0}, {2955., -1.5, 
  0}, {2910.68, -1.5, 0}, {2867.01, -1.5, 0}, {2824.01, -1.5, 
  0}, {2781.65, -1.5, 0}, {2739.92, -1.5, 0}, {2698.83, -1.5, 
  0}, {2658.34, -1.5, 0}, {2618.47, -1.5, 0}, {2579.19, -1.5, 
  0}, {2540.5, -1.5, 0}, {2502.4, -1.5, 0}, {2464.86, -1.5, 
  0}, {2427.89, -1.5, 0}, {2391.47, -1.5, 0}, {2355.6, -1.5, 
  0}, {2320.26, -1.5, 0}, {2285.46, -1.5, 0}, {2251.18, -1.5, 
  0}, {2217.41, -1.5, 12}, {2184.15, -1.5, 63}, {2151.39, -1.5, 
  234}, {2119.12, -1.5, 578}, {2087.33, -1.5, 5210}, {2056.02, -1.5, 
  8919}, {2025.18, -1.5, 9178}, {1994.8, -1.5, 9838}, {1964.88, -1.5, 
  8238}, {1935.41, -1.5, 105}, {1906.37, -1.5, 50}, {1877.78, -1.5, 
  3324}, {1849.61, -1.5, 7783}, {1821.87, -1.5, 8551}, {1794.54, -1.5,
   8996}, {1767.62, -1.5, 8017}, {1741.11, -1.5, 
  1573}, {1714.99, -1.5, 85}, {1689.27, -1.5, 41}, {1663.93, -1.5, 
  7}, {1638.97, -1.5, 4}, {1614.38, -1.5, 4}, {1590.17, -1.5, 
  1}, {1566.32, -1.5, 3}, {1542.82, -1.5, 5}, {1519.68, -1.5, 
  16}, {1496.88, -1.5, 10}, {1474.43, -1.5, 10}, {1452.31, -1.5, 
  13}, {1430.53, -1.5, 3}, {1409.07, -1.5, 2}, {1387.93, -1.5, 
  2}, {1367.12, -1.5, 0}, {1346.61, -1.5, 1}, {1326.41, -1.5, 
  2}, {1306.51, -1.5, 1}, {1286.92, -1.5, 2}, {1267.61, -1.5, 
  0}, {1248.6, -1.5, 0}, {1229.87, -1.5, 0}, {1211.42, -1.5, 
  0}, {1193.25, -1.5, 0}, {1175.35, -1.5, 0}, {1157.72, -1.5, 
  0}, {3000., -1., 0}, {2955., -1., 0}, {2910.68, -1., 
  0}, {2867.01, -1., 0}, {2824.01, -1., 0}, {2781.65, -1., 
  0}, {2739.92, -1., 0}, {2698.83, -1., 0}, {2658.34, -1., 
  0}, {2618.47, -1., 0}, {2579.19, -1., 0}, {2540.5, -1., 
  0}, {2502.4, -1., 0}, {2464.86, -1., 0}, {2427.89, -1., 
  0}, {2391.47, -1., 0}, {2355.6, -1., 0}, {2320.26, -1., 
  0}, {2285.46, -1., 0}, {2251.18, -1., 1}, {2217.41, -1., 
  43}, {2184.15, -1., 301}, {2151.39, -1., 1005}, {2119.12, -1., 
  10636}, {2087.33, -1., 17697}, {2056.02, -1., 18973}, {2025.18, -1.,
   18348}, {1994.8, -1., 14384}, {1964.88, -1., 477}, {1935.41, -1., 
  116}, {1906.37, -1., 7703}, {1877.78, -1., 21245}, {1849.61, -1., 
  23288}, {1821.87, -1., 23861}, {1794.54, -1., 20591}, {1767.62, -1.,
   4015}, {1741.11, -1., 211}, {1714.99, -1., 81}, {1689.27, -1., 
  6}, {1663.93, -1., 8}, {1638.97, -1., 5}, {1614.38, -1., 
  3}, {1590.17, -1., 10}, {1566.32, -1., 11}, {1542.82, -1., 
  24}, {1519.68, -1., 24}, {1496.88, -1., 25}, {1474.43, -1., 
  12}, {1452.31, -1., 5}, {1430.53, -1., 2}, {1409.07, -1., 
  1}, {1387.93, -1., 1}, {1367.12, -1., 7}, {1346.61, -1., 
  1}, {1326.41, -1., 4}, {1306.51, -1., 4}, {1286.92, -1., 
  3}, {1267.61, -1., 1}, {1248.6, -1., 0}, {1229.87, -1., 
  0}, {1211.42, -1., 0}, {1193.25, -1., 0}, {1175.35, -1., 
  0}, {1157.72, -1., 0}, {3000., -0.5, 0}, {2955., -0.5, 
  0}, {2910.68, -0.5, 0}, {2867.01, -0.5, 0}, {2824.01, -0.5, 
  0}, {2781.65, -0.5, 0}, {2739.92, -0.5, 0}, {2698.83, -0.5, 
  0}, {2658.34, -0.5, 0}, {2618.47, -0.5, 0}, {2579.19, -0.5, 
  0}, {2540.5, -0.5, 0}, {2502.4, -0.5, 0}, {2464.86, -0.5, 
  0}, {2427.89, -0.5, 1}, {2391.47, -0.5, 1}, {2355.6, -0.5, 
  0}, {2320.26, -0.5, 2}, {2285.46, -0.5, 5}, {2251.18, -0.5, 
  24}, {2217.41, -0.5, 169}, {2184.15, -0.5, 1859}, {2151.39, -0.5, 
  26781}, {2119.12, -0.5, 32355}, {2087.33, -0.5, 
  31812}, {2056.02, -0.5, 30073}, {2025.18, -0.5, 
  23019}, {1994.8, -0.5, 1463}, {1964.88, -0.5, 975}, {1935.41, -0.5, 
  22077}, {1906.37, -0.5, 41172}, {1877.78, -0.5, 
  41237}, {1849.61, -0.5, 38916}, {1821.87, -0.5, 
  28169}, {1794.54, -0.5, 4424}, {1767.62, -0.5, 369}, {1741.11, -0.5,
   139}, {1714.99, -0.5, 7}, {1689.27, -0.5, 7}, {1663.93, -0.5, 
  5}, {1638.97, -0.5, 3}, {1614.38, -0.5, 4}, {1590.17, -0.5, 
  37}, {1566.32, -0.5, 45}, {1542.82, -0.5, 57}, {1519.68, -0.5, 
  55}, {1496.88, -0.5, 31}, {1474.43, -0.5, 10}, {1452.31, -0.5, 
  2}, {1430.53, -0.5, 2}, {1409.07, -0.5, 0}, {1387.93, -0.5, 
  10}, {1367.12, -0.5, 6}, {1346.61, -0.5, 5}, {1326.41, -0.5, 
  6}, {1306.51, -0.5, 1}, {1286.92, -0.5, 0}, {1267.61, -0.5, 
  0}, {1248.6, -0.5, 0}, {1229.87, -0.5, 0}, {1211.42, -0.5, 
  0}, {1193.25, -0.5, 0}, {1175.35, -0.5, 0}, {1157.72, -0.5, 
  0}, {3000., 0., 0}, {2955., 0., 0}, {2910.68, 0., 0}, {2867.01, 0., 
  0}, {2824.01, 0., 0}, {2781.65, 0., 0}, {2739.92, 0., 0}, {2698.83, 
  0., 0}, {2658.34, 0., 0}, {2618.47, 0., 0}, {2579.19, 0., 
  0}, {2540.5, 0., 2}, {2502.4, 0., 0}, {2464.86, 0., 0}, {2427.89, 
  0., 2}, {2391.47, 0., 1}, {2355.6, 0., 6}, {2320.26, 0., 
  10}, {2285.46, 0., 14}, {2251.18, 0., 84}, {2217.41, 0., 
  656}, {2184.15, 0., 30607}, {2151.39, 0., 34547}, {2119.12, 0., 
  31680}, {2087.33, 0., 28681}, {2056.02, 0., 21817}, {2025.18, 0., 
  4058}, {1994.8, 0., 777}, {1964.88, 0., 31453}, {1935.41, 0., 
  52879}, {1906.37, 0., 50019}, {1877.78, 0., 42382}, {1849.61, 0., 
  26909}, {1821.87, 0., 4682}, {1794.54, 0., 320}, {1767.62, 0., 
  117}, {1741.11, 0., 11}, {1714.99, 0., 8}, {1689.27, 0., 
  6}, {1663.93, 0., 3}, {1638.97, 0., 15}, {1614.38, 0., 
  54}, {1590.17, 0., 76}, {1566.32, 0., 61}, {1542.82, 0., 
  45}, {1519.68, 0., 30}, {1496.88, 0., 6}, {1474.43, 0., 
  10}, {1452.31, 0., 5}, {1430.53, 0., 2}, {1409.07, 0., 3}, {1387.93,
   0., 4}, {1367.12, 0., 4}, {1346.61, 0., 4}, {1326.41, 0., 
  2}, {1306.51, 0., 1}, {1286.92, 0., 0}, {1267.61, 0., 0}, {1248.6, 
  0., 0}, {1229.87, 0., 0}, {1211.42, 0., 0}, {1193.25, 0., 
  0}, {1175.35, 0., 0}, {1157.72, 0., 0}, {3000., 0.5, 0}, {2955., 
  0.5, 0}, {2910.68, 0.5, 0}, {2867.01, 0.5, 0}, {2824.01, 0.5, 
  0}, {2781.65, 0.5, 0}, {2739.92, 0.5, 0}, {2698.83, 0.5, 
  0}, {2658.34, 0.5, 0}, {2618.47, 0.5, 0}, {2579.19, 0.5, 
  0}, {2540.5, 0.5, 0}, {2502.4, 0.5, 0}, {2464.86, 0.5, 1}, {2427.89,
   0.5, 2}, {2391.47, 0.5, 4}, {2355.6, 0.5, 11}, {2320.26, 0.5, 
  12}, {2285.46, 0.5, 42}, {2251.18, 0.5, 289}, {2217.41, 0.5, 
  27382}, {2184.15, 0.5, 30705}, {2151.39, 0.5, 27644}, {2119.12, 0.5,
   24207}, {2087.33, 0.5, 17481}, {2056.02, 0.5, 3848}, {2025.18, 0.5,
   165}, {1994.8, 0.5, 25344}, {1964.88, 0.5, 49338}, {1935.41, 0.5, 
  45039}, {1906.37, 0.5, 33975}, {1877.78, 0.5, 18053}, {1849.61, 0.5,
   2646}, {1821.87, 0.5, 196}, {1794.54, 0.5, 57}, {1767.62, 0.5, 
  8}, {1741.11, 0.5, 2}, {1714.99, 0.5, 1}, {1689.27, 0.5, 
  1}, {1663.93, 0.5, 5}, {1638.97, 0.5, 39}, {1614.38, 0.5, 
  66}, {1590.17, 0.5, 58}, {1566.32, 0.5, 36}, {1542.82, 0.5, 
  15}, {1519.68, 0.5, 2}, {1496.88, 0.5, 4}, {1474.43, 0.5, 
  3}, {1452.31, 0.5, 1}, {1430.53, 0.5, 2}, {1409.07, 0.5, 
  1}, {1387.93, 0.5, 4}, {1367.12, 0.5, 0}, {1346.61, 0.5, 
  0}, {1326.41, 0.5, 2}, {1306.51, 0.5, 0}, {1286.92, 0.5, 
  1}, {1267.61, 0.5, 0}, {1248.6, 0.5, 0}, {1229.87, 0.5, 
  0}, {1211.42, 0.5, 0}, {1193.25, 0.5, 0}, {1175.35, 0.5, 
  0}, {1157.72, 0.5, 0}, {3000., 1., 0}, {2955., 1., 0}, {2910.68, 1.,
   0}, {2867.01, 1., 0}, {2824.01, 1., 0}, {2781.65, 1., 0}, {2739.92,
   1., 0}, {2698.83, 1., 1}, {2658.34, 1., 0}, {2618.47, 1., 
  0}, {2579.19, 1., 0}, {2540.5, 1., 0}, {2502.4, 1., 0}, {2464.86, 
  1., 2}, {2427.89, 1., 4}, {2391.47, 1., 11}, {2355.6, 1., 
  13}, {2320.26, 1., 23}, {2285.46, 1., 122}, {2251.18, 1., 
  18319}, {2217.41, 1., 26444}, {2184.15, 1., 20484}, {2151.39, 1., 
  14402}, {2119.12, 1., 4624}, {2087.33, 1., 41}, {2056.02, 1., 
  128}, {2025.18, 1., 19349}, {1994.8, 1., 32847}, {1964.88, 1., 
  22347}, {1935.41, 1., 10553}, {1906.37, 1., 824}, {1877.78, 1., 
  188}, {1849.61, 1., 25}, {1821.87, 1., 6}, {1794.54, 1., 
  2}, {1767.62, 1., 1}, {1741.11, 1., 1}, {1714.99, 1., 1}, {1689.27, 
  1., 2}, {1663.93, 1., 22}, {1638.97, 1., 40}, {1614.38, 1., 
  26}, {1590.17, 1., 13}, {1566.32, 1., 8}, {1542.82, 1., 
  1}, {1519.68, 1., 2}, {1496.88, 1., 0}, {1474.43, 1., 0}, {1452.31, 
  1., 1}, {1430.53, 1., 1}, {1409.07, 1., 2}, {1387.93, 1., 
  0}, {1367.12, 1., 0}, {1346.61, 1., 1}, {1326.41, 1., 0}, {1306.51, 
  1., 0}, {1286.92, 1., 0}, {1267.61, 1., 0}, {1248.6, 1., 
  0}, {1229.87, 1., 0}, {1211.42, 1., 0}, {1193.25, 1., 0}, {1175.35, 
  1., 0}, {1157.72, 1., 0}, {3000., 1.5, 0}, {2955., 1.5, 
  0}, {2910.68, 1.5, 0}, {2867.01, 1.5, 0}, {2824.01, 1.5, 
  0}, {2781.65, 1.5, 0}, {2739.92, 1.5, 0}, {2698.83, 1.5, 
  0}, {2658.34, 1.5, 0}, {2618.47, 1.5, 0}, {2579.19, 1.5, 
  1}, {2540.5, 1.5, 1}, {2502.4, 1.5, 2}, {2464.86, 1.5, 2}, {2427.89,
   1.5, 11}, {2391.47, 1.5, 13}, {2355.6, 1.5, 17}, {2320.26, 1.5, 
  37}, {2285.46, 1.5, 439}, {2251.18, 1.5, 18068}, {2217.41, 1.5, 
  10376}, {2184.15, 1.5, 1429}, {2151.39, 1.5, 21}, {2119.12, 1.5, 
  23}, {2087.33, 1.5, 45}, {2056.02, 1.5, 6339}, {2025.18, 1.5, 
  14719}, {1994.8, 1.5, 6337}, {1964.88, 1.5, 329}, {1935.41, 1.5, 
  114}, {1906.37, 1.5, 9}, {1877.78, 1.5, 5}, {1849.61, 1.5, 
  5}, {1821.87, 1.5, 1}, {1794.54, 1.5, 0}, {1767.62, 1.5, 
  0}, {1741.11, 1.5, 0}, {1714.99, 1.5, 1}, {1689.27, 1.5, 
  5}, {1663.93, 1.5, 11}, {1638.97, 1.5, 8}, {1614.38, 1.5, 
  1}, {1590.17, 1.5, 0}, {1566.32, 1.5, 2}, {1542.82, 1.5, 
  1}, {1519.68, 1.5, 0}, {1496.88, 1.5, 1}, {1474.43, 1.5, 
  1}, {1452.31, 1.5, 1}, {1430.53, 1.5, 0}, {1409.07, 1.5, 
  0}, {1387.93, 1.5, 0}, {1367.12, 1.5, 0}, {1346.61, 1.5, 
  0}, {1326.41, 1.5, 0}, {1306.51, 1.5, 0}, {1286.92, 1.5, 
  0}, {1267.61, 1.5, 0}, {1248.6, 1.5, 0}, {1229.87, 1.5, 
  0}, {1211.42, 1.5, 0}, {1193.25, 1.5, 0}, {1175.35, 1.5, 
  0}, {1157.72, 1.5, 0}, {3000., 2., 0}, {2955., 2., 0}, {2910.68, 2.,
   0}, {2867.01, 2., 0}, {2824.01, 2., 0}, {2781.65, 2., 0}, {2739.92,
   2., 0}, {2698.83, 2., 0}, {2658.34, 2., 0}, {2618.47, 2., 
  0}, {2579.19, 2., 0}, {2540.5, 2., 1}, {2502.4, 2., 2}, {2464.86, 
  2., 4}, {2427.89, 2., 10}, {2391.47, 2., 5}, {2355.6, 2., 
  14}, {2320.26, 2., 22}, {2285.46, 2., 891}, {2251.18, 2., 
  3}, {2217.41, 2., 5}, {2184.15, 2., 3}, {2151.39, 2., 8}, {2119.12, 
  2., 8}, {2087.33, 2., 50}, {2056.02, 2., 102}, {2025.18, 2., 
  2}, {1994.8, 2., 3}, {1964.88, 2., 1}, {1935.41, 2., 2}, {1906.37, 
  2., 1}, {1877.78, 2., 0}, {1849.61, 2., 1}, {1821.87, 2., 
  1}, {1794.54, 2., 0}, {1767.62, 2., 0}, {1741.11, 2., 0}, {1714.99, 
  2., 0}, {1689.27, 2., 0}, {1663.93, 2., 1}, {1638.97, 2., 
  0}, {1614.38, 2., 0}, {1590.17, 2., 0}, {1566.32, 2., 0}, {1542.82, 
  2., 0}, {1519.68, 2., 0}, {1496.88, 2., 0}, {1474.43, 2., 
  0}, {1452.31, 2., 0}, {1430.53, 2., 0}, {1409.07, 2., 0}, {1387.93, 
  2., 0}, {1367.12, 2., 0}, {1346.61, 2., 0}, {1326.41, 2., 
  0}, {1306.51, 2., 0}, {1286.92, 2., 0}, {1267.61, 2., 0}, {1248.6, 
  2., 0}, {1229.87, 2., 0}, {1211.42, 2., 0}, {1193.25, 2., 
  0}, {1175.35, 2., 0}, {1157.72, 2., 0}, {3000., 2.5, 0}, {2955., 
  2.5, 0}, {2910.68, 2.5, 0}, {2867.01, 2.5, 0}, {2824.01, 2.5, 
  0}, {2781.65, 2.5, 0}, {2739.92, 2.5, 0}, {2698.83, 2.5, 
  1}, {2658.34, 2.5, 0}, {2618.47, 2.5, 1}, {2579.19, 2.5, 
  0}, {2540.5, 2.5, 1}, {2502.4, 2.5, 4}, {2464.86, 2.5, 2}, {2427.89,
   2.5, 1}, {2391.47, 2.5, 0}, {2355.6, 2.5, 1}, {2320.26, 2.5, 
  1}, {2285.46, 2.5, 1}, {2251.18, 2.5, 2}, {2217.41, 2.5, 
  0}, {2184.15, 2.5, 0}, {2151.39, 2.5, 0}, {2119.12, 2.5, 
  0}, {2087.33, 2.5, 0}, {2056.02, 2.5, 0}, {2025.18, 2.5, 
  0}, {1994.8, 2.5, 0}, {1964.88, 2.5, 0}, {1935.41, 2.5, 
  0}, {1906.37, 2.5, 0}, {1877.78, 2.5, 0}, {1849.61, 2.5, 
  0}, {1821.87, 2.5, 0}, {1794.54, 2.5, 0}, {1767.62, 2.5, 
  0}, {1741.11, 2.5, 0}, {1714.99, 2.5, 0}, {1689.27, 2.5, 
  0}, {1663.93, 2.5, 0}, {1638.97, 2.5, 0}, {1614.38, 2.5, 
  0}, {1590.17, 2.5, 0}, {1566.32, 2.5, 0}, {1542.82, 2.5, 
  0}, {1519.68, 2.5, 0}, {1496.88, 2.5, 0}, {1474.43, 2.5, 
  0}, {1452.31, 2.5, 0}, {1430.53, 2.5, 0}, {1409.07, 2.5, 
  0}, {1387.93, 2.5, 0}, {1367.12, 2.5, 0}, {1346.61, 2.5, 
  0}, {1326.41, 2.5, 0}, {1306.51, 2.5, 0}, {1286.92, 2.5, 
  0}, {1267.61, 2.5, 0}, {1248.6, 2.5, 0}, {1229.87, 2.5, 
  0}, {1211.42, 2.5, 0}, {1193.25, 2.5, 0}, {1175.35, 2.5, 
  0}, {1157.72, 2.5, 0}, {3000., 3., 0}, {2955., 3., 0}, {2910.68, 3.,
   0}, {2867.01, 3., 0}, {2824.01, 3., 0}, {2781.65, 3., 0}, {2739.92,
   3., 0}, {2698.83, 3., 0}, {2658.34, 3., 0}, {2618.47, 3., 
  0}, {2579.19, 3., 0}, {2540.5, 3., 0}, {2502.4, 3., 0}, {2464.86, 
  3., 0}, {2427.89, 3., 0}, {2391.47, 3., 0}, {2355.6, 3., 
  0}, {2320.26, 3., 0}, {2285.46, 3., 0}, {2251.18, 3., 0}, {2217.41, 
  3., 0}, {2184.15, 3., 0}, {2151.39, 3., 0}, {2119.12, 3., 
  0}, {2087.33, 3., 0}, {2056.02, 3., 0}, {2025.18, 3., 1}, {1994.8, 
  3., 0}, {1964.88, 3., 0}, {1935.41, 3., 0}, {1906.37, 3., 
  0}, {1877.78, 3., 0}, {1849.61, 3., 0}, {1821.87, 3., 0}, {1794.54, 
  3., 0}, {1767.62, 3., 0}, {1741.11, 3., 0}, {1714.99, 3., 
  0}, {1689.27, 3., 0}, {1663.93, 3., 1}, {1638.97, 3., 0}, {1614.38, 
  3., 0}, {1590.17, 3., 0}, {1566.32, 3., 0}, {1542.82, 3., 
  0}, {1519.68, 3., 0}, {1496.88, 3., 0}, {1474.43, 3., 0}, {1452.31, 
  3., 0}, {1430.53, 3., 0}, {1409.07, 3., 0}, {1387.93, 3., 
  0}, {1367.12, 3., 0}, {1346.61, 3., 0}, {1326.41, 3., 0}, {1306.51, 
  3., 0}, {1286.92, 3., 0}, {1267.61, 3., 0}, {1248.6, 3., 
  0}, {1229.87, 3., 0}, {1211.42, 3., 0}, {1193.25, 3., 0}, {1175.35, 
  3., 0}, {1157.72, 3., 0}, {3000., 3.5, 0}, {2955., 3.5, 
  0}, {2910.68, 3.5, 0}, {2867.01, 3.5, 0}, {2824.01, 3.5, 
  0}, {2781.65, 3.5, 0}, {2739.92, 3.5, 0}, {2698.83, 3.5, 
  0}, {2658.34, 3.5, 0}, {2618.47, 3.5, 0}, {2579.19, 3.5, 
  0}, {2540.5, 3.5, 0}, {2502.4, 3.5, 0}, {2464.86, 3.5, 0}, {2427.89,
   3.5, 0}, {2391.47, 3.5, 0}, {2355.6, 3.5, 0}, {2320.26, 3.5, 
  0}, {2285.46, 3.5, 0}, {2251.18, 3.5, 0}, {2217.41, 3.5, 
  0}, {2184.15, 3.5, 0}, {2151.39, 3.5, 0}, {2119.12, 3.5, 
  0}, {2087.33, 3.5, 0}, {2056.02, 3.5, 0}, {2025.18, 3.5, 
  0}, {1994.8, 3.5, 0}, {1964.88, 3.5, 0}, {1935.41, 3.5, 
  0}, {1906.37, 3.5, 0}, {1877.78, 3.5, 0}, {1849.61, 3.5, 
  0}, {1821.87, 3.5, 0}, {1794.54, 3.5, 0}, {1767.62, 3.5, 
  0}, {1741.11, 3.5, 0}, {1714.99, 3.5, 0}, {1689.27, 3.5, 
  0}, {1663.93, 3.5, 0}, {1638.97, 3.5, 0}, {1614.38, 3.5, 
  0}, {1590.17, 3.5, 0}, {1566.32, 3.5, 0}, {1542.82, 3.5, 
  0}, {1519.68, 3.5, 0}, {1496.88, 3.5, 0}, {1474.43, 3.5, 
  0}, {1452.31, 3.5, 0}, {1430.53, 3.5, 0}, {1409.07, 3.5, 
  0}, {1387.93, 3.5, 0}, {1367.12, 3.5, 0}, {1346.61, 3.5, 
  0}, {1326.41, 3.5, 0}, {1306.51, 3.5, 0}, {1286.92, 3.5, 
  0}, {1267.61, 3.5, 0}, {1248.6, 3.5, 0}, {1229.87, 3.5, 
  0}, {1211.42, 3.5, 0}, {1193.25, 3.5, 0}, {1175.35, 3.5, 
  0}, {1157.72, 3.5, 0}, {3000., 4., 0}, {2955., 4., 0}, {2910.68, 4.,
   0}, {2867.01, 4., 0}, {2824.01, 4., 0}, {2781.65, 4., 0}, {2739.92,
   4., 0}, {2698.83, 4., 0}, {2658.34, 4., 0}, {2618.47, 4., 
  0}, {2579.19, 4., 0}, {2540.5, 4., 0}, {2502.4, 4., 0}, {2464.86, 
  4., 0}, {2427.89, 4., 0}, {2391.47, 4., 0}, {2355.6, 4., 
  0}, {2320.26, 4., 0}, {2285.46, 4., 0}, {2251.18, 4., 0}, {2217.41, 
  4., 0}, {2184.15, 4., 0}, {2151.39, 4., 0}, {2119.12, 4., 
  0}, {2087.33, 4., 0}, {2056.02, 4., 0}, {2025.18, 4., 0}, {1994.8, 
  4., 0}, {1964.88, 4., 0}, {1935.41, 4., 0}, {1906.37, 4., 
  0}, {1877.78, 4., 0}, {1849.61, 4., 0}, {1821.87, 4., 0}, {1794.54, 
  4., 0}, {1767.62, 4., 0}, {1741.11, 4., 0}, {1714.99, 4., 
  0}, {1689.27, 4., 0}, {1663.93, 4., 0}, {1638.97, 4., 0}, {1614.38, 
  4., 0}, {1590.17, 4., 0}, {1566.32, 4., 0}, {1542.82, 4., 
  0}, {1519.68, 4., 0}, {1496.88, 4., 0}, {1474.43, 4., 0}, {1452.31, 
  4., 0}, {1430.53, 4., 0}, {1409.07, 4., 0}, {1387.93, 4., 
  0}, {1367.12, 4., 0}, {1346.61, 4., 0}, {1326.41, 4., 0}, {1306.51, 
  4., 0}, {1286.92, 4., 0}, {1267.61, 4., 0}, {1248.6, 4., 
  0}, {1229.87, 4., 0}, {1211.42, 4., 0}, {1193.25, 4., 0}, {1175.35, 
  4., 0}, {1157.72, 4., 0}};

Check out MorphologicalComponents[data] and related. This will isolate the two thresholded regions — OpticsMan, Jan 17 '23 at 22:00

score 3 · Answer 1 · answered Jan 18 '23 at 10:09

3

I like the answer by yarchik, but I think it is better to utilize MorphologicalComponents without using functions and interpolation.

arr = GatherBy[data, #[[2]] &];
arr2 = Map[#[[3]] &, arr, {2}];
ArrayPlot[arr2]
img = Image[arr2/Max[arr2]]
Colorize[MorphologicalComponents[img, 0.3], ImageSize -> Medium]
{peak1, peak2} = 
  Part[arr, Sequence @@ #] & /@ 
     Position[MorphologicalComponents[img, 0.3], #] & /@ {1, 2};
ListPointPlot3D[{peak1, peak2}, PlotLegends -> Automatic]

answered Jan 18 '23 at 10:09

Anton Antonov

37,787
3
100
178

1

Very nice, I was not happy myself with interpolation. It is much better to use MorphologicalComponents with a threshold parameter as you did. – yarchik Jan 18 '23 at 10:19

score 2 · Answer 2 · answered Jan 18 '23 at 08:55

2

The problem is the non-homogeneous mesh of your data and the noise that is not visible in your plot. One can filter the data to remove noise and interpolate it on the regular mesh

data2 = Table[{u[[1]], u[[2]], If[u[[3]] < 25000, 0, u[[3]]]}, {u, 
    data}];
f2 = Interpolation[data2, InterpolationOrder -> 1]
data3 = Table[f2[x, y], {x, 1160, 3000, 40}, {y, -4, 4, 0.5}];
Colorize[MorphologicalComponents[data3], ImageSize -> Medium]

answered Jan 18 '23 at 08:55

yarchik

18,202
2
28
66

If Log[data[[All,1]] is used instead of data[[All,1]], the mesh is pretty uniform. – JimB Jan 18 '23 at 17:36

score 2 · Answer 3 · answered Jan 18 '23 at 18:35

Here is a "model assisted" approach if it is reasonable to assume that you have a random sample from a mixture distribution consisting of two bivariate normal distributions.

Also note that taking the log of the voltage results in a uniform grid of points.

First get rid of the zero counts.

data0 = data;
data0[[All, 1]] = Log[data[[All, 1]]];
data0 = Select[data0, #[[3]] > 0 &];

Define a mixture distribution of two bivariate normal distributions.

d = MixtureDistribution[{p, 1 - p}, {BinormalDistribution[{μ11, μ12}, {σ11, σ12}, ρ1],
    BinormalDistribution[{μ21, μ22}, {σ21, σ22}, ρ2]}];

Construct the log of (an approximation of) the likelihood.

logL = 0;
Do[logL = logL + data0[[i, 3]] LogLikelihood[d, {data0[[i, {1, 2}]]}], {i, Length[data0]}]

Find maximum likelihood estimates of parameters.

mle = FindMaximum[{logL, {σ11 > 0, σ12 > 0, σ21 > 0, σ22 > 0, -1 < ρ1 < 1, -1 < ρ2 < 1, 0 < p < 1}},
  {{σ11, 0.04}, {σ21, 0.04}, {σ12, 1.5}, {σ22, 1.5}, {ρ1, 0.8}, {ρ2, 0.8}, 
  {μ11, 7.5}, {μ12, 0}, {μ21, 7.7}, {μ22, 0}, {p, 0.5}}]
(* {902840., {σ11 -> 0.0348575, σ21 -> 0.0337503, σ12 -> 0.734831, σ22 -> 0.807352,
    ρ1 -> 0.782644, ρ2 -> 0.78997, μ11 -> 7.55199, μ12 -> -0.0499241, 
    μ21 -> 7.65925, μ22 -> -0.0607625, p -> 0.549756}} *)

Show resulting bivariate probability density.

Plot3D[PDF[d /. mle[[2]], {logVoltage, angle}], {logVoltage, Log[1500], Log[2500]}, {angle, -3, 3},
  PlotRange -> All, PlotPoints -> 100, 
  AxesLabel -> {"Log[voltage]", "Angle", "Probability\ndensity"}]

Define a function that gives the ratio of the likelihoods. If the ratio is greater than 1, assign the point to data set 1, otherwise assign a point to data set 2.

f[voltage_, angle_, mle_] := 
  PDF[BinormalDistribution[{μ11, μ12}, {σ11, σ12}, ρ1], {Log[voltage], angle}]/
  PDF[BinormalDistribution[{μ21, μ22}, {σ21, σ22}, ρ2], {Log[voltage], angle}]/. mle
data1 = data;
data2 = data;
Do[If[f[data[[i, 1]], data[[i, 2]], mle[[2]]] > 1, data2[[i, 3]] = 0, 
  data1[[i, 3]] = 0], {i, Length[data]}]

Show the resulting density plots for each data set.

ListDensityPlot[data1, PlotRange -> All]
ListDensityPlot[data2, PlotRange -> All]

score 1 · Accepted Answer · answered Jan 18 '23 at 10:15

We try to create two masks that will filter out the peaks.

First we create a mask that filters both peaks, using a threshold of 1000 (you may change this as needed):

mask0 = {#[[1]], #[[2]], If[#[[3]] > 1000, 1, 0]} & /@ data;

This will get the two peaks. To separate the peaks, we define a line by two points (can be changed as needed) and define a function that indicates on which side of the line a third point is:

p1 = {1740, -4};
p2 = {2250, 4};
side[p0_, p1_, p2_] := 
  Sign[(p1[[1]] - p0[[1]]) (p2[[2]] - p0[[2]]) - (p1[[2]] - 
       p0[[2]]) (p2[[1]] - p0[[1]])];

With this we can now define masks for the two peaks:

mask1 = ({#[[1]], #[[2]], #[[3]] If[side[p1, p2, #[[;; 2]]] == 1, 1, 
        0]}) & /@ mask0;
mask2 = ({#[[1]], #[[2]], #[[3]] If[side[p1, p2, #[[;; 2]]] == 1, 0, 
        1]}) & /@ mask0;

To separate the peaks and draw them:

data1 = MapThread[{#1[[1]], #1[[2]], #1[[3]] #2[[3]]} &, {data, 
    mask1}];
ListPlot3D[data1, PlotRange -> All]
data2 = MapThread[{#1[[1]], #1[[2]], #1[[3]] #2[[3]]} &, {data, 
    mask2}];
ListPlot3D[data2, PlotRange -> All]

Separating two peaks in a 2D array of data

4 Answers4