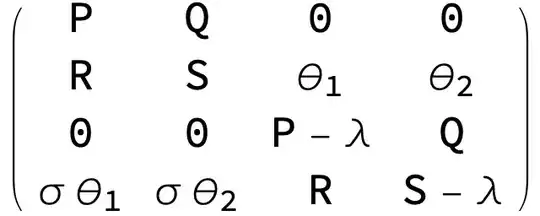
Basically I am trying to find symbolic eigenvalues of a 4x4 Matrix. Using the below code
{P, Q, 0, 0},
{R, S, Subscript[θ, 1], Subscript[θ, 2]},
{0, 0 , P - λ, Q},
{σ Subscript[θ, 1], σ Subscript[θ, 2],
R, S - λ}
} );
X = Eigenvalues[M]
I expect to get the answer in a formated form, but instead I am getting the expression.
{Root[Q^2 R^2 - 2 P Q R S + P^2 S^2 + P Q R λ -
P^2 S λ + Q R S λ - P S^2 λ -
Q R λ^2 +
P S λ^2 + (-2 P - 2 S + 2 λ) #1^3 + #1^4 -
Q^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(1\), \(2\)]\) +
2 P Q σ Subscript[θ, 1] Subscript[θ, 2] -
Q λ σ Subscript[θ, 1] Subscript[θ,
2] - P^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) +
P λ σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) + #1^2 (P^2 -
2 Q R + 4 P S + S^2 - 3 P λ -
3 S λ + λ^2 - σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) + #1 (2 P Q R \
- 2 P^2 S + 2 Q R S - 2 P S^2 + P^2 λ - 2 Q R λ +
4 P S λ + S^2 λ - P λ^2 -
S λ^2 -
2 Q σ Subscript[θ, 1] Subscript[θ, 2] +
2 P σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) - λ \
σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) &, 1],
Root[Q^2 R^2 - 2 P Q R S + P^2 S^2 + P Q R λ -
P^2 S λ + Q R S λ - P S^2 λ -
Q R λ^2 +
P S λ^2 + (-2 P - 2 S + 2 λ) #1^3 + #1^4 -
Q^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(1\), \(2\)]\) +
2 P Q σ Subscript[θ, 1] Subscript[θ, 2] -
Q λ σ Subscript[θ, 1] Subscript[θ,
2] - P^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) +
P λ σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) + #1^2 (P^2 -
2 Q R + 4 P S + S^2 - 3 P λ -
3 S λ + λ^2 - σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) + #1 (2 P Q R \
- 2 P^2 S + 2 Q R S - 2 P S^2 + P^2 λ - 2 Q R λ +
4 P S λ + S^2 λ - P λ^2 -
S λ^2 -
2 Q σ Subscript[θ, 1] Subscript[θ, 2] +
2 P σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) - λ \
σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) &, 2],
Root[Q^2 R^2 - 2 P Q R S + P^2 S^2 + P Q R λ -
P^2 S λ + Q R S λ - P S^2 λ -
Q R λ^2 +
P S λ^2 + (-2 P - 2 S + 2 λ) #1^3 + #1^4 -
Q^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(1\), \(2\)]\) +
2 P Q σ Subscript[θ, 1] Subscript[θ, 2] -
Q λ σ Subscript[θ, 1] Subscript[θ,
2] - P^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) +
P λ σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) + #1^2 (P^2 -
2 Q R + 4 P S + S^2 - 3 P λ -
3 S λ + λ^2 - σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) + #1 (2 P Q R \
- 2 P^2 S + 2 Q R S - 2 P S^2 + P^2 λ - 2 Q R λ +
4 P S λ + S^2 λ - P λ^2 -
S λ^2 -
2 Q σ Subscript[θ, 1] Subscript[θ, 2] +
2 P σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) - λ \
σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) &, 3],
Root[Q^2 R^2 - 2 P Q R S + P^2 S^2 + P Q R λ -
P^2 S λ + Q R S λ - P S^2 λ -
Q R λ^2 +
P S λ^2 + (-2 P - 2 S + 2 λ) #1^3 + #1^4 -
Q^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(1\), \(2\)]\) +
2 P Q σ Subscript[θ, 1] Subscript[θ, 2] -
Q λ σ Subscript[θ, 1] Subscript[θ,
2] - P^2 σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) +
P λ σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) + #1^2 (P^2 -
2 Q R + 4 P S + S^2 - 3 P λ -
3 S λ + λ^2 - σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) + #1 (2 P Q R \
- 2 P^2 S + 2 Q R S - 2 P S^2 + P^2 λ - 2 Q R λ +
4 P S λ + S^2 λ - P λ^2 -
S λ^2 -
2 Q σ Subscript[θ, 1] Subscript[θ, 2] +
2 P σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\) - λ \
σ
\!\(\*SubsuperscriptBox[\(θ\), \(2\), \(2\)]\)) &, 4]}
However, if I assign numerical values to all the constants used and then use the command ClearAll["Global`*"];
and repeat the cell execution, I am getting the expected result (Formatted Math) which in Input form corresponds to
{1/2 (P + S - Sqrt[P^2 + 4 Q R - 2 P S + S^2]),
1/2 (P + S + Sqrt[P^2 + 4 Q R - 2 P S + S^2]),
1/2 (P + S - Sqrt[P^2 + 4 Q R - 2 P S + S^2] - 2 λ),
1/2 (P + S + Sqrt[P^2 + 4 Q R - 2 P S + S^2] - 2 λ)}
Which is what I wanted. I do not understand why assigning numerical values and then clearing them seems to solve the problem. Is there any way to avoid the problem in the first place? Note - The same problem does not occur when I take an arbitrary symbolic 2x2 matrix.