Extracting the major and minor axes values from the elliptic equation

Question

If the equation of ellipse is:

$$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,$$

then how can the major and minor axes values in the denominators be extracted from eq?

eq = x^2/4 + y^2/3 == 1;

a^2=4; a=2; b^2=3; b=sqrt(3)

Answer 1

Expressing the ellipse as eq == 0:

eq = x^2/4 + y^2/3 - 1;

The semi-major axes are calculated from the eigenvalues of the second derivatives of eq:

1/Sqrt[Eigenvalues[D[eq, {{x, y}, 2}]/2]] // NumericalSort
(*    {Sqrt[3], 2}    *)

This is more general than pattern-matching approaches and also works on rotated ellipses:

eq = x^2/4 + x y/7 + y^2/3 - 1;
1/Sqrt[Eigenvalues[D[eq, {{x, y}, 2}]/2]] // NumericalSort
(*    {2 Sqrt[42/(49 + Sqrt[193])], 2 Sqrt[42/(49 - Sqrt[193])]}    *)

Answer 2

eq1 = x^2/4 + y^2/3 == 1;
eq2 = x^2/a^2 + y^2/b^2 == 1;
Solve[Denominator[Flatten@(List @@@ List @@ eq1)] == 
  Denominator[Flatten@(List @@@ List @@ eq2)], 
 Assumptions -> {a > 0 && b > 0}]

{{a -> 2, b -> Sqrt[3]}}

Answer 3

Another possibility is (*8 more left to do *)

ClearAll["Global`*"]
eq = x^2/4 + y^2/3 == 1;
normalized = First[eq] - Last[eq]

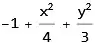
Coefficient[normalized, x^Exponent[normalized, x]];
Sqrt[Denominator[%]]  (*a*)

Coefficient[normalized, y^Exponent[normalized, y]];
Sqrt[Denominator[%]]  (*b*)

---

If the exponent is not meant to be the max but only 2 then do

ClearAll["Global`*"]
eq = x^2/4 + y^2/3 == 1;
normalized = First[eq] - Last[eq]
Sqrt[Denominator[Coefficient[normalized, x^2]]] (*a*)
Sqrt[Denominator[Coefficient[normalized, y^2]]] (*b*)

Answer 4

eq = x^2/4 + y^2/3 == 1;
TreeForm[eq]

To extract the coefficients:

(1/Sqrt[#]) &@(First /@ Level[eq, {2}])

{2, Sqrt[3]}

Answer 5

try https://resources.wolframcloud.com/FunctionRepository/resources/EllipseProperties

ass = ResourceFunction["EllipseProperties"][x^2/4 + y^2/3 == 1, {x, y}];
ass["SemimajorAxisLength"]
ass["SemiminorAxisLength"]

2

Sqrt[3]