How to subtract these two equations?

Question

There are two equations:

eq1 = x1^2/a^2 + y1^2/b^2 == 1;
eq2 = x2^2/a^2 + y2^2/b^2 == 1;

How to get this result by subtracting two equations?

the result

((x1 - x2) (x1 + x2))/a^2 + ((y1 - y2) (y1 + y2))/b^2 == 0

score 8 · Accepted Answer · answered Jan 28 '23 at 12:27

subtracting two equations?

You can use SubtractSides which is designed for this sort of operation.

ClearAll["Global`*"]
eq1 = x1^2/a^2 + y1^2/b^2 == 1
eq2 = x2^2/a^2 + y2^2/b^2 == 1
SubtractSides[eq1, eq2]

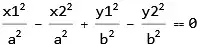
Mathematica graphics

To simplify it more

SubtractSides[eq1, eq2] // Simplify

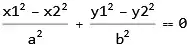
Mathematica graphics

Without using this command, there are other ways to do this. See Subtracting equations from each other? for more options.

Syed · Answer 2 · 2023-01-28T13:37:25.037

4

(eq1 - eq2 /. Equal -> List // Equal @@ # & // 
   Collect[#, {a, b}] &) /. (a_^2 - b_^2) :> (a + b) (a - b)

$$\frac{(\text{x1}-\text{x2}) (\text{x1}+\text{x2})}{a^2}+\frac{(\text{y1}-\text{y2}) (\text{y1}+\text{y2})}{b^2}$$

edited Jan 28 '23 at 13:37

answered Jan 28 '23 at 13:18

Syed

52,495
4
30
85

Could you have a look at my SDE question: https://mathematica.stackexchange.com/questions/276606/numerically-solving-a-system-of-sdes-with-levy-noise?noredirect=1#comment697578_276606. Thank you! – Math Jan 30 '23 at 12:52
@Math, I don't have enough expertise in that area. The most qualified participants have already looked at it. If you have another question, it is best to start a fresh post. Thanks. – Syed Jan 30 '23 at 13:30
No problem, Thank you anyway :) – Math Jan 30 '23 at 13:46

score 3 · Answer 3 · answered Jan 28 '23 at 16:32

Try also this:

eq1 = x1^2/a^2 + y1^2/b^2 == 1;
eq2 = x2^2/a^2 + y2^2/b^2 == 1;
expr=Equal @@ MapThread[Subtract, {List @@ eq1, List @@ eq2}] // Simplify
(*  (x1^2 - x2^2)/a^2 + (y1^2 - y2^2)/b^2 == 0  *)

If you need them factorized:

MapAt[Factor, expr, {{1, 1}, {1, 2}}]
(*  ((x1 - x2) (x1 + x2))/a^2 + ((y1 - y2) (y1 + y2))/b^2 == 0  *)

Have fun!

score 3 · Answer 4 · answered Jan 28 '23 at 23:18

3

Another way to do this is as follows:

FullSimplify[Thread[#[[1]] == #[[2]]] &@(#[[1]] - #[[2]] & /@ 
Transpose[Level[#, {1}] & /@ {eq1, eq2}])]

answered Jan 28 '23 at 23:18

E. Chan-López

23,117
3
21
44

score 0 · Answer 5 · answered Jan 30 '23 at 22:27

eq1 = x1^2/a^2 + y1^2/b^2 == 1;
eq2 = x2^2/a^2 + y2^2/b^2 == 1;

Original way

eq1 - eq2 // Thread[#, Equals] & // Simplify
(* (x1^2-x2^2)/a^2+(y1^2-y2^2)/b^2==0 *)

If you use EqualThread found at https://library.wolfram.com/infocenter/MathSource/4491, then it will be seamless.

eq1 - eq2//Simplify

to get the same answer.

How to subtract these two equations?

5 Answers5

Linked