Solving a system of fractional differential equations

Question

I have adopted the method in the link to solve a much simpler system but it takes ages to execute.

a1 = 2/3; b1 = 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8;
\[Alpha] = 1; h = .0025;
tau = 0.15; nn = Round[tau/h]; smax = Round[15/tau]; n = nn*smax;
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y;
Do[x[i] = x0; y[i] = y0, {i, -nn, 0}];
For[k = 1, k <= n, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha] ;
a[k] = -(2*k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k +
1)^([Alpha] + 1);];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, snn}];
For[j = 1, j <= snn, j++,
p[j] = (h^[Alpha]Sum[b[j - A]f[Ah, x[A], y[A]], {A, 0, j - 1}])/
Gamma[[Alpha] + 1] + x[0];
l[j] = (h^[Alpha]
Sum[b[j - B]g[Bh, x1[B], y[B]], {B, 0, j - 1}])/
Gamma[[Alpha] + 1] + y[0];
x[j] = (h^[Alpha](Sum[
a[j - K]f[hK, x[K], y1[K]], {K, 1, j - 1}] +
f[hj, p[j],
l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)*
j^[Alpha])f[0, x[0], y[0]]))/Gamma[[Alpha] + 2] + x[0];
y[j] = (h^[Alpha](Sum[
a[j - F]g[Fh, x1[F], y[F]], {F, 1, j - 1}] +
g[hj, p[j],
l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)
j^[Alpha])*g[0, x[0], y[0]]))/Gamma[[Alpha] + 2] +
y[0];];, {s, 1, smax}]
lst1 = Table[{x[j], y[j]}, {j, n}];
lst = Table[{x[j], y[j]}, {j, 10, n, 10}];
Clear[x, y];
sol = NDSolve[{x'[t] == f[t, x[t], y[t - tau]],
y'[t] == g[t, x[t - tau], y[t]], x[t /; t <= 0] == 0.9,
y[t /; t <= 0] == 1.8}, {x, y}, {t, 0, 40}];
{Show[ParametricPlot[{x[t], y[t]} /. sol[[1]], {t, .0, 20},
PlotRange -> All, Frame -> True, FrameLabel -> {x, y}],
ListPlot[lst1, PlotStyle -> Red, PlotRange -> All, Frame -> True]]}

Moreover for smaller steps and for alpha other than 1, the solution doesnt make anysense.

Could you add more written explanation of your problem? And what does "FDEs" stand for - fractional differential equations, functional differential equations, fuzzy differential equations, or something else? — Chris K, Jan 31 '23 at 02:07

Alex Trounev · Accepted Answer · 2023-02-03T16:42:39.733

There is a typo in the code. We should use y1[A] in p[j] definition. Also for $\alpha<1$ we should take very small step h, since predictor-corrector algorithm depends on $h^{\alpha}$. For example, if for $\alpha =1$ solution converges at $h=0.01$, then for $\alpha =1/2$ solution converges at $h=10^{-4}$. To test code we put $h=1/100, \alpha =1, 4/5$. As benchmark solution we use NDSolve at $\alpha=1$, so we have

Clear[x, y];
a1 = 2/3; b1 = 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8;
\[Alpha] = 1; h = .01; par1 = h^\[Alpha]/Gamma[\[Alpha] + 1]; par2 = 
 h^\[Alpha]/Gamma[\[Alpha] + 2];
tau = 0.15; nn = Round[tau/h]; n = 40 nn;
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y;
Do[x[i] = x0; y[i] = y0, {i, -nn, 0}];
For[k = 1, k <= n, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha];
  a[k] = -(2*k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k + 
       1)^([Alpha] + 1);];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, snn}];
  For[j = 1, j <= snn, j++, 
   p[j] = (par1 Sum[b[j - A]f[Ah, x[A], y1[A]], {A, 0, j - 1}]) + 
     x[0];
   l[j] = (par1 Sum[b[j - B]g[Bh, x1[B], y[B]], {B, 0, j - 1}]) + 
     y[0];
   x[j] = (par2 (Sum[a[j - K]f[hK, x[K], y1[K]], {K, 1, j - 1}] + 
         f[hj, p[j], 
          l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)
             j^[Alpha])f[0, x[0], y[0]])) + x[0];
   y[j] = (par2 (Sum[a[j - F]g[Fh, x1[F], y[F]], {F, 1, j - 1}] + 
         g[hj, p[j], 
          l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)*
             j^[Alpha])*g[0, x[0], y[0]])) + y[0];];, {s, 1, 
   40}] // AbsoluteTiming
lst1 = Table[{x[j], y[j]}, {j, n}];
Clear[x, y];
[Alpha] = 4/5; h = .01; par1 = h^[Alpha]/Gamma[[Alpha] + 1]; par2 =
  h^[Alpha]/Gamma[[Alpha] + 2];
tau = 0.15; nn = Round[tau/h]; n = 40 nn;
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y;
Do[x[i] = x0; y[i] = y0, {i, -nn, 0}];
For[k = 1, k <= n, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha];
  a[k] = -(2*k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k + 
       1)^([Alpha] + 1);];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, snn}];
  For[j = 1, j <= snn, j++, 
   p[j] = (par1 Sum[b[j - A]f[Ah, x[A], y1[A]], {A, 0, j - 1}]) + 
     x[0];
   l[j] = (par1 Sum[b[j - B]g[Bh, x1[B], y[B]], {B, 0, j - 1}]) + 
     y[0];
   x[j] = (par2 (Sum[a[j - K]f[hK, x[K], y1[K]], {K, 1, j - 1}] + 
         f[hj, p[j], 
          l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)
             j^[Alpha])f[0, x[0], y[0]])) + x[0];
   y[j] = (par2 (Sum[a[j - F]g[Fh, x1[F], y[F]], {F, 1, j - 1}] + 
         g[hj, p[j], 
          l[j]] + ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)*
             j^[Alpha])*g[0, x[0], y[0]])) + y[0];];, {s, 1, 
   40}] // AbsoluteTiming
lst2 = Table[{x[j], y[j]}, {j, n}];
Clear[x, y];
a1 = 2/3; b1 = 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8; 
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y; tau = 0.15;
sol = NDSolve[{x'[t] == f[t, x[t], y[t - tau]], 
    y'[t] == g[t, x[t - tau], y[t]], x[t /; t <= 0] == 0.9, 
    y[t /; t <= 0] == 1.8}, {x, y}, {t, 0, 40}];
pl1 = ParametricPlot[{x[t], y[t]} /. sol[[1]], {t, .0, n h}, 
   PlotRange -> All, Frame -> True, FrameLabel -> {x, y}, 
   AspectRatio -> 1/2, PlotStyle -> Green];

Visualization

Show[pl1, ListLinePlot[lst1, PlotStyle -> {Red, Dashed}], 
 ListLinePlot[lst2, PlotStyle -> {Blue, Dashed}]]

With small modification of the code above we can compute up to t=15 as follows

a1 = 2/3; b1 = 
 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8; \[Alpha] = 1; h = .01; par1 \
= h^\[Alpha]/Gamma[\[Alpha] + 1]; par2 = 
 h^\[Alpha]/Gamma[\[Alpha] + 2];
tau = 0.15; nn = Round[tau/h]; smax = 100; n = smax nn;
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y;
Do[x[i] = x0; y[i] = y0, {i, -nn, 0}]; f0 = f[0, x[0], y[0]]; g0 = 
 g[0, x[0], y[0]];
For[k = 1, k <= n, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha];
  a[k] = -(2k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k + 
       1)^([Alpha] + 1); 
  c[k] = ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)j^[Alpha])];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, snn}];
  For[j = 1, j <= snn, j++, bj = Table[b[j - A], {A, 0, j - 1}]; 
   f1j = Table[f[Ah, x[A], y1[A]], {A, 0, j - 1}]; 
   p[j] = par1 bj . f1j + x[0]; 
   g1j = Table[g[Bh, x1[B], y[B]], {B, 0, j - 1}];
   l[j] = par1 bj . g1j + y[0]; aj = Table[a[j - i], {i, 1, j - 1}]; 
   f2j = Table[f[hKk, x[Kk], y1[Kk]], {Kk, 1, j - 1}];
   x[j] = par2 (aj . f2j + f[hj, p[j], l[j]] + c[j] f0) + x[0]; 
   g2j = Table[g[Fh, x1[F], y[F]], {F, 1, j - 1}];
   y[j] = 
    par2 (aj . g2j + g[hj, p[j], l[j]] + c[j] g0) + y[0];];, {s, 1, 
   smax}] // AbsoluteTiming

This part with $\alpha=1$ takes 444s on my laptop.

lst1 = Table[{x[j], y[j]}, {j, n}];
Clear[x, y];
a1 = 2/3; b1 = 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8; [Alpha] = 
 4/5; h = .01; par1 = h^[Alpha]/Gamma[[Alpha] + 1]; par2 = 
 h^[Alpha]/Gamma[[Alpha] + 2];
tau = 0.15; nn = Round[tau/h]; n = smax nn;
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y;
Do[x[i] = x0; y[i] = y0, {i, -nn, 0}];
f0 = f[0, x[0], y[0]]; g0 = g[0, x[0], y[0]];
For[k = 1, k <= n, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha];
  a[k] = -(2k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k + 
       1)^([Alpha] + 1); 
  c[k] = ((j - 1)^([Alpha] + 1) - (-[Alpha] + j - 1)j^[Alpha])];
Do[Do[x1[i] = x[i - nn]; y1[i] = y[i - nn];, {i, 0, snn}];
  For[j = 1, j <= snn, j++, bj = Table[b[j - A], {A, 0, j - 1}]; 
   f1j = Table[f[Ah, x[A], y1[A]], {A, 0, j - 1}]; 
   p[j] = par1 bj . f1j + x[0]; 
   g1j = Table[g[Bh, x1[B], y[B]], {B, 0, j - 1}];
   l[j] = par1 bj . g1j + y[0]; aj = Table[a[j - i], {i, 1, j - 1}]; 
   f2j = Table[f[hKk, x[Kk], y1[Kk]], {Kk, 1, j - 1}];
   x[j] = par2 (aj . f2j + f[hj, p[j], l[j]] + c[j] f0) + x[0]; 
   g2j = Table[g[Fh, x1[F], y[F]], {F, 1, j - 1}];
   y[j] = 
    par2 (aj . g2j + g[hj, p[j], l[j]] + c[j] g0) + y[0];];, {s, 1, 
   smax}] // AbsoluteTiming

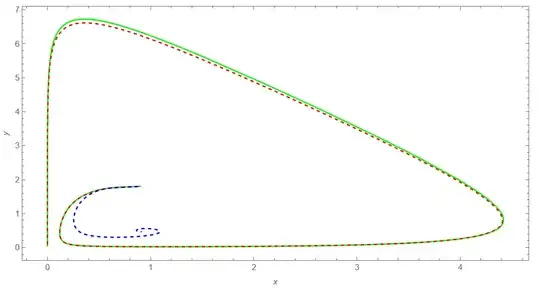
Part with $\alpha=4/5$ takes 739s. Why this code so slow compare to NDSolve? Actually we solve the system of delay integrodifferential equations, while with NDSolve we solve DDEs. Visualization

Clear[x, y];
a1 = 2/3; b1 = 4/3; c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8; 
f[t_, x_, y_] := a1x - b1xy;
g[t_, x_, y_] := c1xy - d1y; tau = 0.15;
sol = NDSolve[{x'[t] == f[t, x[t], y[t - tau]], 
    y'[t] == g[t, x[t - tau], y[t]], x[t /; t <= 0] == 0.9, 
    y[t /; t <= 0] == 1.8}, {x, y}, {t, 0, 15}];
pl1 = ParametricPlot[{x[t], y[t]} /. sol[[1]], {t, .0, n h}, 
   PlotRange -> All, Frame -> True, FrameLabel -> {x, y}, 
   AspectRatio -> 1/2, PlotStyle -> Green];
Show[pl1, 
 ListLinePlot[lst1, PlotStyle -> {Red, Dashed}, PlotRange -> Full], 
 ListLinePlot[lst2, PlotStyle -> {Blue, Dashed}, PlotRange -> Full]]

Update 1. This problem also can be solved with wavelets collocation method. In the code below we use Haar wavelets. The main limitation of this algorithm is FindRoot usage. In this example we use 32 collocation points to compute system of fractional DDE with $\alpha=q=4/5$ up to t=tmax=10. It takes about 15s on my laptop.

tmax = 10; n = 4; q = 8/10; a1 = 2/3; b1 = 4/3; c1 = 1;
  d1 = 1; x0 = 0.9; y0 = 1.8; tau = 0.15;
 M = Sum[1, {j, 0, n, 1}, {i, 0, 2^j - 1, 1}] + 1; dx = 1/M; 
 xl = Table[l dx, {l, 0, M}]; 
 xcol = Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, M + 1}]; 
 xcolN = xcol - 1.*10^-10;
 psi1[x_] := WaveletPsi[HaarWavelet[], x];
 psi2[x_] := WaveletPhi[HaarWavelet[], x];
 psi1jk[x_, j_, k_] := psi1[j x - k];
 psi2jk[x_, j_, k_] := psi2[j x - k];
 psijk[x_, j_, k_] := Sqrt[j] (psi1jk[x, j, k] + psi2jk[x, j, k]); 
 p1i = Table[
   Flatten[Table[
     NIntegrate[psijk[t, 2^j, k], {t, 0, xcol[[i]]}], {j, 0, n, 
      1}, {k, 0, 2^j - 1, 1}]], {i, Length[xcol]}]; 
 pci = Table[
   Flatten[Table[
     NIntegrate[
      psijk[t, 2^j, k]/(xcol[[i]] - t)^q, {t, 0, xcolN[[i]]}], {j, 0, 
      n, 1}, {k, 0, 2^j - 1, 1}]], {i, Length[xcol]}];
 var = Table[
   Flatten[Table[b[i, j, k], {j, 0, n, 1}, {k, 0, 2^j - 1, 1}]], {i, 
    2}]; ic = {.9, 1.8};
 fp = Table[
   Table[var[[j]] . p1i[[i]] + b0[j] xcol[[i]] + ic[[j]], {i, 
     Length[xcol]}], {j, 2}]; 
 fpc = Table[
   Table[var[[j]] . pci[[i]] + b0[j] xcol[[i]]^(1 - q)/(1 - q), {i, 
     Length[xcol]}], {j, 2}]; tn = (1/tmax)^q/Gamma[1 - q];
 p1tau = 
  Table[Flatten[
    Table[NIntegrate[
      psijk[t - tau/tmax, 2^j, k], {t, 0, xcol[[i]]}], {j, 0, n, 
      1}, {k, 0, 2^j - 1, 1}]], {i, Length[xcol]}]; 
 fptau = Table[
   Table[var[[j]] . p1tau[[i]] + b0[j] xcol[[i]] + ic[[j]], {i, 
     Length[xcol]}], {j, 2}];
 eq1 = Table[-fpc[[1, i]] tn + a1*fp[[1, i]] - 
     b1*fp[[1, i]]*fptau[[2, i]] == 0, {i, Length[xcol]}]; 
 eq2 = Table[-fpc[[2, i]] tn - d1*fp[[2, i]] + 
     c1*fp[[2, i]]*fptau[[1, i]] == 0, {i, Length[xcol]}];
 varM = Join[var[[1]], var[[2]], {b0[1], b0[2]}]; 
 sol1 = FindRoot[{eq1, eq2}, 
   Table[{varM[[i]], 1/10}, {i, Length[varM]}]];

Visualization along and together with Figure 2

lst = Join[{ic}, 
   Table[{fp[[1, i]], fp[[2, i]]} /. sol1, {i, Length[xcol]}]]; 
ListPlot[lst, PlotRange -> Full, PlotStyle -> {Red, PointSize[.015]}, 
 AxesLabel -> {"x", "y"}]

Update 2. We can improve code above using exact solution for Caputo derivative from here as follows

AbsoluteTiming[
 h[x_, k_, m_] := 
  WaveletPsi[HaarWavelet[], m x - k, WorkingPrecision -> Infinity];
 p[x_, k_, m_] := 
  Piecewise[{{(1 + k - m*x)/m, 
     k >= 0 && 1/m + (2*k)/m - 2*x < 0 && 1/m + k/m - x >= 0 && 
      m > 0}, {(-k + m*x)/m, 
     k >= 0 && 1/m + (2*k)/m - 2*x >= 0 && k/m - x < 0 && 
      1/m + k/m - x >= 0 && m > 0}}, 0];
 h1[x_] := 
  WaveletPhi[HaarWavelet[], x, WorkingPrecision -> Infinity];
 p1[x_] := Piecewise[{{1, x > 1}}, x];
 pc[t_, k_, m_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     k == 0 && 1/m - 2*t >= 0 && m > 0 && t > 0 && 
      1/m - t >= 
       0}, {-((m^(-1 + q)*(1/(-k + m*t))^(-1 + q))/(-1 + q)), 
     k > 0 && 1/m + (2*k)/m - 2*t > 0 && k/m - t < 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {(-t^q + 2*m*t^(1 + q) - 
        m*t*(-(1/(2*m)) + t)^q)/(t^q*(-(1/(2*m)) + t)^q*(m*(-1 + q))),
      k == 0 && m > 0 && 1/m - 2*t < 0 && 
      1/m - t >= 
       0}, {(1/(-1 + q))*((2^(-1 + q)*
          m^(-1 + 2*q)*(-(-(k/m) + t)^q - 2*k*(-(k/m) + t)^q + 
            2*m*t*(-(k/m) + t)^q + 2*k*(-((1/2 + k)/m) + t)^q - 
            2*m*t*(-((1/2 + k)/m) + t)^q))/((1 + 2*k - 2*m*t)*(k - 
             m*t))^q), 
     k > 0 && 1/m + (2*k)/m - 2*t == 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {-((1/(-1 + q))*((2^(-1 + q)*
            m^(-1 + 2*q)*(-2*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q - 
              2*k*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + 
              2*m*t*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^
                q + (-((1 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + 
              2*k*(-((1 + k)/m) + t)^q*((1 + 2*k - 2*m*t)*(k - m*t))^
                q - 2*m*t*(-((1 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + (-(k/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q + 
              2*k*(-(k/m) + t)^q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^
                q - 2*m*t*(-(k/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q - 
              2*k*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q + 
              2*m*t*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^
                q))/(((1 + 2*k - 2*m*t)*(k - m*t))^
             q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q))), 
     k > 0 && m > 0 && 1/m + (2*k)/m - 2*t <= 0 && 
      1/m + k/m - t <= 
       0}, {-((1/(2*
            m*(-1 + q)))*((2^q*m^(2*q)*
             t^q*(-(1/m) + t)^q*(-(1/(2*m)) + t)^q - 
            2^(1 + q)*m^(1 + 2*q)*
             t^(1 + q)*(-(1/m) + t)^q*(-(1/(2*m)) + t)^q - 
            2^(1 + q)*m^(2*q)*t^q*(-(1/(2*m)) + t)^(2*q) + 
            2^(1 + q)*m^(1 + 2*q)*t^(1 + q)*(-(1/(2*m)) + t)^(2*q) + 
            t^q*((-1 + m*t)*(-1 + 2*m*t))^q - 
            2*m*t^(1 + q)*((-1 + m*t)*(-1 + 2*m*t))^q + 
            2*m*t*(-(1/(2*m)) + t)^q*((-1 + m*t)*(-1 + 2*m*t))^q)/(t^
             q*(-(1/(2*m)) + t)^q*((-1 + m*t)*(-1 + 2*m*t))^q))), 
     k == 0 && 1/m - 2*t < 0 && 1/m - t < 0 && 
      m > 0}, {(1/(-1 + q))*((2^(-1 + q)*
          m^(-1 + q)*((-m^q)*(-(k/m) + t)^q - 
            2*k*m^q*(-(k/m) + t)^q + 2*m^(1 + q)*t*(-(k/m) + t)^q + 
            2*k*m^q*(-((1/2 + k)/m) + t)^q - 
            2*m^(1 + q)*
             t*(-((1/2 + k)/m) + t)^q - ((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q - 
            2*k*((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q + 
            2*m*t*((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q))/((1 + 2*k - 2*m*t)*(k - 
             m*t))^q), 
     1/m + (2*k)/m - 2*t < 0 && k > 0 && m > 0 && 1/m + k/m - t > 0}},
    0];
pc1[t_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     t <= 1}}, -(((-1 + t)^qt + t^q - t^(1 + q))/((-1 + t)^q
        t^q*(-1 + q)))];
 tmax = 10; q = 8/10; tn = 1/tmax^q/Gamma[1 - q]; a1 = 2/3; b1 = 4/3; 
 c1 = 1; d1 = 1; x0 = 0.9; y0 = 1.8; tau = 0.15; J = 5; M = 2^J; 
 dx = 1/(2*M); xl = Table[l dx, {l, 0, 2 M}]; 
 xcol = Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, 2 M + 1}];
 x1[t_, q_] := 
  Sum[v[i, j] pc[t, i, 2^j, q], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   v1 pc1[t, q];
 x[t_] := 
  Sum[v[i, j] p[t, i, 2^j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   v1 p1[t] + v0;
 y1[t_, q_] := 
  Sum[u[i, j] pc[t, i, 2^j, q], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   u1 pc1[t, q];
 y[t_] := 
  Sum[u[i, j] p[t, i, 2^j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   u1 p1[t] + u0;
 varM = Join[{v0, v1, u0, u1}, 
   Flatten[Table[v[i, j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}]], 
   Flatten[Table[u[i, j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}]]];
 eq[q_] := 
  Flatten[
   Table[{-x1[t, q] tn + a1 x[t] - b1 x[t] y[t - tau/tmax] == 
      0, -y1[t, q] tn - d1 y[t] + c1 y[t] x[t - tau/tmax] == 0}, {t, 
     xcol}]]; ic = {x[0] == .9, y[0] == 1.8};
 sol = FindRoot[Join[eq[q], ic], 
   Table[{varM[[i]], 1/10}, {i, Length[varM]}]];]

It takes 4s only for 64 collocation points. As a bonus we have interpolation function for x[t], y[t]. Visualization

ParametricPlot[{x[t], y[t]} /. sol, {t, 0, 1}, PlotRange -> All, 
 AspectRatio -> 1/2, PlotStyle -> {Red, Dashed}, Frame -> True, 
 FrameLabel -> {"x", "y"}]

Thansk for your response. Can you please try to check the result for {t,0,15} for both alpha=1 and alpha=4/5? — zhk, Feb 01 '23 at 07:46
@zhk Actually we don't know, but we can try to solve this problem using the Euler wavelets collocation method and compare time with predictor-corrector algorithm. — Alex Trounev, Feb 02 '23 at 03:28
@zhk Please, see Update 1 to my answer. In this example code with wavelets 30 times faster than predictor-corrector algorithm. — Alex Trounev, Feb 02 '23 at 12:53
Thanks for your efforts. Can you please use Wavelets to solve the diffusion equation in cylindrical coordinates given in this post https://mathematica.stackexchange.com/questions/276896/ — zhk, Feb 03 '23 at 04:09
It would be more convenient if the final solution are represented by interpolating functions. — zhk, Feb 03 '23 at 12:38

Solving a system of fractional differential equations

1 Answers1