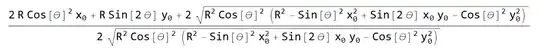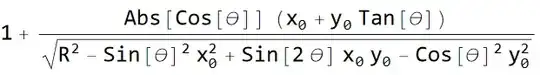0

I'm trying to solve for the derivative of [Psi] with respect to [Theta] from these two equations:

Eqn1a = R*Cos[Subscript[\[Psi], 1][\[Theta]]] == Subscript[x, 0] + p[\[Theta]]*Cos[\[Theta]]
Eqn1b = R*Sin[Subscript[\[Psi], 1][\[Theta]]] == Subscript[y, 0] + p[\[Theta]]*Sin[\[Theta]]

I want to find the derivative in terms of x_0, y_0 and [Theta]. In other words, I want to eliminate the variables p and the derivative of p. I've tried differentiating both equations and then using Solve but I've been unsuccessful.

Eqn1aD = D[Eqn1a, \[Theta]]
Eqn1bD = D[Eqn1b, \[Theta]]
sol = Solve[{Eqn1a, Eqn1b},Derivative[1][Subscript[\[Psi], 1]][\[Theta]]]
Matthew James
  • 23
  • 4

1 Answers1

2

I am not sure that I understood you completely. For example, is it OK with you if one solves the initial system with respect to Psi1(theta) and p(theta) and then finds the derivative of Psi1(theta)? If it is OK, try the following:

sol = Solve[{Eqn1a, Eqn1b}, {Subscript[\[Psi], 1][\[Theta]],p[\[Theta]]}] /. C[1] -> 0 // Simplify;

expr=D[sol[[1, 2, 2]], [Theta]] // Simplify

with the following effect:

enter image description here

The same operation one can apply to the second solution.

Edit The result has already been simplified. However, addressing the question of @Matthew James one can customize the resulting expression assuming that the expression staying under the radical is positive:

Map[Simplify[#, {R^2 Cos[\[Theta]]^2 (R^2 - Sin[\[Theta]]^2 
\!\(\*SubsuperscriptBox[\(x\), \(0\), \(2\)]\) + 
         Sin[2 \[Theta]] Subscript[x, 0] Subscript[y, 0] - 
         Cos[\[Theta]]^2 
\!\(\*SubsuperscriptBox[\(y\), \(0\), \(2\)]\)) > 0, R > 0}] &, 
  expr // Expand] // Simplify

The latter result is easier to look at if I post it as an image:

enter image description here

Have fun!

Alexei Boulbitch
  • 39,397
  • 2
  • 47
  • 96