5

I am trying to mesh the following domain to solve a heat transfer + fluid flow problem:

computational domain

The continuity+momentum equations are to be solved in $ABGH$, while the energy equation is to be solved across the entire domain, i.e., $ABCDEFGH$ (basically line $CF$ is the solid-fluid interface). To generate mesh for $ABGH$, I used the following:

Needs["MeshTools`"]
L = 0.050, d = 0.003, e = 0.005, delta = 0.010, l = L/d + 2 delta/d
mesh = ToElementMesh[FullRegion[2], {{0, l}, {0, 1}}, MaxCellMeasure -> 8 10^-3];

(ElementMesh[{{0., 23.3333}, {0., 1.}}, {QuadElement["<" 3132 ">"]}])

which produces the following:

ABGH mesh

Now, to mesh the entire domain, I use the tool StructuredMesh in the following code (about which I learned from the various answers on this post):

raster = {{{0, 0}, {delta/d, 0}, {delta/d, -e/d}, {delta/d + L/d, -e/d}, {delta/d + L/d, 0}, {l, 0}}, {{0, 1}, {delta/d, 1}, {delta + L/(3 d), 1}, {delta + (2 L/(3 d)), 1}, {delta/d + L/d, 1}, {l, 1}}}
mesh2 = StructuredMesh[raster, {200, 20}]
mesh2["Wireframe"]
(*ElementMesh[{{0., 23.3333}, {-1.66667, 1.}}, {QuadElement["<" 4000 ">"]}]*)

This produces the following:

ABCDEFGH mesh

To produce this, I have basically defined the domain using two lines, each having six points through the raster command. However, as visible the mesh quality is pretty bad.

How should the $ABCDEFGH$ domain be meshed to achieve a smooth quad mesh as $ABGH$? Also, it will be beneficial if I can have the same number of elements in the ABGH portion, while meshing ABCDEFGH as it had when it was individually meshed.

Also, this leads me to think, can both these sub-domains be meshed separetly and then joined?

Update 1 Upon recommendations in the comment, I tried the following:

MergeMesh for different size domains work on BoundaryMesh type object. Atleast, that is what I found in the documentation.

Needs["NDSolve`FEM`"]
Needs["MeshTools`"]
{L = 0.050, d = 0.003, e = 0.005, delta = 0.010, l = L/d + 2 delta/d};
reg1 = ImplicitRegion[0 <= x <= l && 0 <= y <= 1, {x, y}];
reg2 = ImplicitRegion[
   delta/d <= x <= l - delta/d && -e/d <= y <= 0, {x, y}];
reg3 = RegionUnion[reg1, reg2];

bm1 = ToBoundaryMesh[reg1]
bm2 = ToBoundaryMesh[reg2]
bm3 = MergeMesh[{bm1, bm2}]
meshfluid = ToElementMesh[bm1, MaxCellMeasure -> 0.01]["Wireframe"]
meshenergy = ToElementMesh[bm3, MaxCellMeasure -> 0.01]["Wireframe"]
(meshsolid = ToElementMesh[bm2, MaxCellMeasure -> 0.01]["Wireframe"])

This leads to the following:

meshenergy_triangular

However, this is a triangular mesh. TriangleToQuadMesh does not work on meshenergy object. Also if you see the image above closely, the refinement at the interface (i.e., internal boundary) is localised to a few regions. Also MeshCellCount does not work when I try it on meshenergy, meshfluid or meshsolid.

Update 2

A comparison among tri and quad mesh results

I used the answer given here by Oleksii, to solve the problem of conjugate heat transfer (reciprocating flow over a heated block). Obviously, I have utlised the domain described in this question. Both the cases have been run for a flow time of 5 seconds, with similar MaxStepSize setting

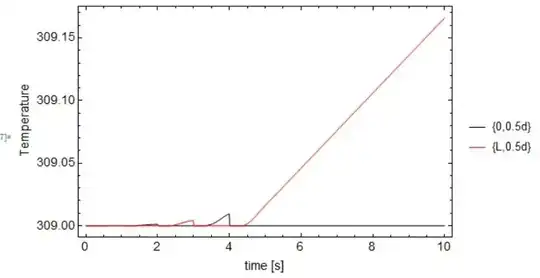
Triangular mesh results

Created using the Update 1 in this question.

Please note that ToElementMesh creates a 2nd order mesh. To interpolate the p which is supplied with p->1 in NDSolve, I had to create a 1st order mesh using MeshOrderAlteration

  1. Mesh statistics

enter image description here

  1. Solid temperature variation at point ((delta+L)/d/2,-e/d/2)

enter image description here

  1. Fluid temperature variation at both the inlets of the fluid domain

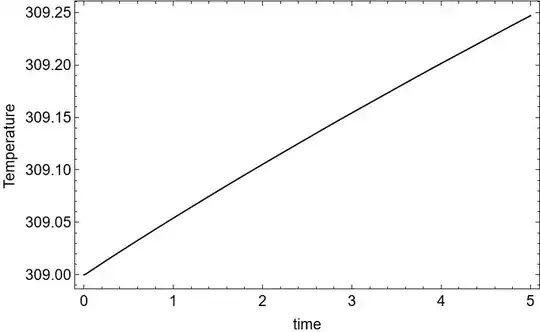
enter image description here

Quad mesh results

Mesh generated using Oleksii's answer in this question

Similar number of elements in y-direction in the fluid domain (compared to trimesh) could be achieved with the setting NyF. Hence, total number of elements is lesser than trimesh.

  1. Mesh statistics

enter image description here

  1. Solid temperature variation at point ((delta+L)/d/2,-e/d/2)

enter image description here

  1. Fluid temperature variation at both the inlets of the fluid domain

enter image description here

In conclusion, the results seem fairly simialr. I will run these tests for longer flow times and report if there are any discrepancies that arise. However, it seems quadmesh allows more control over element size in such regular domains (thus leading to lesser total element count).

Addendum to Update 2 The following contour plots, show the difference in solution between the quad and triangle mesh (at the same flow time). Please note that the triangle mesh is generated using the answer of @user21.

Solid temperature

enter image description here

Fluid temperature Have replaced AspectRatio->Automatic to AspectRatio->1/2, as the fluid region is thin.

enter image description here

Note: Total elements for triangle mesh: 3246 Total elements for quad mesh: 1248

user21
  • 39,710
  • 8
  • 110
  • 167
Avrana
  • 297
  • 1
  • 4
  • 14
  • 1
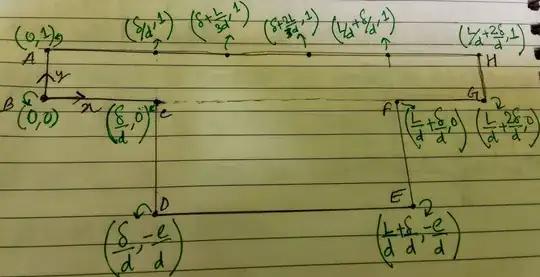
    You can try to build uniform meshes separately for fluid and solid domains and then to join them by MergeMesh from MeshTools – Oleksii Semenov Feb 04 '23 at 12:11
  • @OleksiiSemenov I gave it a try. See Update. – Avrana Feb 04 '23 at 13:08
  • 1
    Great. A few comments. You should not use the mesh from update 1 - this already looks bad and I suspect it has holes or some such. For the triangular mesh use the mesh that I used for the quad mesh generation. – user21 Feb 10 '23 at 08:31
  • 1
    If you want to put in the work, what would be much more informative is to plot the difference between the solutions. But again, for this type of problem I would not expect much of a difference in the solution. Triangle elements are typically a bit more efficient to evaluate. – user21 Feb 10 '23 at 08:33
  • @user21 Thankyou for the comments. See "Addendum to Update 2". The fluid domain shows considerable difference it seems. – Avrana Feb 11 '23 at 03:36
  • @user21 On another note, (this is in context to the linked question, where the problem is described) I had to put an insulated region before the heated length 0 to delta/d, to circumvent the issue of pinning that happens if a constant Dirichlet condition (fluid inlet) shares a node with a Neumann condition (solid edge). For such scenarios COMSOL uses an Inflow boundary condition, which models the fluid inlet as a flux condition. – Avrana Feb 11 '23 at 03:57
  • You can read about the description of the Inflow condition here. Can such b.c. be implemented as part of Mathematica NDSolve in future? This becomes important when conduction heat transfer near the inlet is not dominated by advective heat transfer., i.e., Low Re flows and small dimensions. – Avrana Feb 11 '23 at 03:58
  • @Avrana, I had quick look at the link, which of the equations (number) are you interested in? To me it looks like they are variants of NeuamnnValues and it should be possible to do this today; if I have understood things correctly. One other thing you might want to do is add your requests (a thickness parameter for the heat equation and/or this inflow condition) here. – user21 Feb 13 '23 at 07:47

2 Answers2

7

Function MergeMesh from MeshTools package allows to join separate meshes. Let's take advantage of this useful function for this problem.

Needs["MeshTools`"]
L = 0.050; d = 0.003; e = 0.005; delta = 0.010; 
l = L/d + 2 delta/d;

NxS = 40;
NyS = 10;
MeshSolid = 
  RectangleMesh[{delta/d, -e/d}, {(L + delta)/d, 0}, {NxS, NyS}];


NxF = 10;
NyF = 10;
MeshFluid1 = RectangleMesh[{0, 0}, {delta/d, 1}, {NxF, NyF}];
MeshFluid2 = RectangleMesh[{(delta + L)/d, 0}, {l, 1}, {NxF, NyF}];
MeshFluid3 = RectangleMesh[{(delta)/d, 0}, {(L + delta)/d, 1}, {NxS, NyF}];
MeshFluid = MergeMesh[MergeMesh[MeshFluid1, MeshFluid3], MeshFluid2]


MeshTotal = MergeMesh[MeshFluid, MeshSolid];
MeshTotal["Wireframe"]

FEmesh

Oleksii Semenov
  • 1,187
  • 6
  • 11
  • Much much thanks. This is exactly what I wanted. I wasnt aware of the RectangleMesh function too. Keeping similar NxS probably helped. I would also like to ask, if such rectangle meshes are better for fluid flow problems ? – Avrana Feb 04 '23 at 19:20
  • @Avrana, it would be interesting to hear what you find when you use this mesh in place of a triangulated region. I doubt it is going to make much of a difference, but I could be wrong. – user21 Feb 06 '23 at 14:49
  • 1
    @Avrana I will respond on your question about tri mesh vs quads mesh a little bit later. It is blackout in my city now and I am on smartphone – Oleksii Semenov Feb 06 '23 at 15:23
  • @user21 I will post some results in some time. On move right now. – Avrana Feb 07 '23 at 09:42
  • 1
    @Avrana about tri mesh vs quad mesh in cfd. It is popular debatable issue. And as far as I know the choice of proper mesh depends on particular problem in question. May be this work https://www.researchgate.net/publication/339311266_Mesh_Assessment_Quality_Issues will be interesting for you. As concerns the problem you are working on, I think you should carry out the computational experiments with different meshes and then make a choice. Interesting to look at these results. – Oleksii Semenov Feb 07 '23 at 21:23
  • 1
    @Avrana The points ${\frac{\delta}{d},0}$ and ${\frac{L+\delta}{d},0}$ are certainly the trouble spots where the large temperature gradients appears. And it would be better to make gradual mesh refinement there. – Oleksii Semenov Feb 07 '23 at 21:28
  • @OleksiiSemenov Thankyou for the comments. I have been away, so could not review them earlier. Please look at Update 2 in my question, presenting a comparison among tri and quad mesh results using your last answer here. You can see, I have added an insulated portion before the heated length. This is to resolve the problem of pinning in the previous domain shape, where the Dirichlet boundary (fluid) had shared nodes with Neumann boundary (solid edge). – Avrana Feb 10 '23 at 04:46
  • I will go through the reference you have suggested. Thank you. – Avrana Feb 10 '23 at 04:55
  • @user21 I have updated the question with a comparison between tri and quad mesh results, as requested. Have a look. – Avrana Feb 10 '23 at 04:55
4

A different approach might be to use ToQuadMesh:

Needs["FEMAddOns`"]
L = 0.050; d = 0.003; e = 0.005; delta = 0.010; l = L/d + 2 delta/d;
bmesh = ToBoundaryMesh[
   "Coordinates" -> {{0, 0}, {delta/d, 
      0}, {delta/d, -e/d}, {delta/d + L/d, -e/d}, {delta/d + L/d, 
      0}, {2*delta/d + L/d, 0}, {L/d + 2*delta/d, 1}, {0, 1}}, 
   "BoundaryElements" -> {LineElement[{{1, 2}, {2, 3}, {3, 4}, {4, 
        5}, {5, 6}, {6, 7}, {7, 8}, {8, 1}, {2, 5}}]}];
bmesh["Wireframe"]

enter image description here

mesh = ToElementMesh[bmesh];
quadMesh = ToQuadMesh[mesh];
quadMesh["Wireframe"]

enter image description here

Not, quite what you were looking for but perhaps an alternative option. Note, that the internal boundary is not respected by ToQuadMesh. If you specify region markers then it works:

mesh = ToElementMesh[bmesh, 
   "RegionMarker" -> {{{L/2, 0.9}, 1, 1}, {{L/2, 0.1}, 1, 2}}];
quadMesh = ToQuadMesh[mesh];
quadMesh["Wireframe"]

enter image description here

user21
  • 39,710
  • 8
  • 110
  • 167
  • Thankyou for this. I will test this mesh too. I hope the RegionMarker can be used to assign separate properties to each zone? – Avrana Feb 10 '23 at 04:48
  • 2
    The RegionMarker can indeed do this. The documentation gives some pretty good examples of use cases. – Dunlop Feb 10 '23 at 05:33