Error in Euler wavelets collocation method

Question

I have adopted the code given here. But it produces an error.

NDSolve solution

eqns = {CaputoD[w[y, t], {t, a}] == D[w[y, t], {y, 2}],
    CaputoD[T[y, t], {t, a}] ==
    D[T[y, t], {y, 2}] + D[w[y, t], {y, 1}]^2};
    ics = {w[y, 0] == 0, T[y, 0] == 0};
    bcs = {w[0, t] == Cos[t], T[0, t] == 1, w[1, t] == 0,
    T[1, t] == 0}; var = {w, T}; sol1 =
    NDSolveValue[{eqns, ics, bcs} /. a -> 1, var, {y, 0, 1}, {t, 0, 10}];
    Table[Plot3D[sol1[[i]][y, t], {y, 0, 1}, {t, 0, 1},
    ColorFunction -> Hue, AxesLabel -> Automatic,
    PlotLabel -> var[[i]]], {i, 2}]

wavelets method

UE[m_, t_] := EulerE[m, t];
psi[k_, n_, m_, t_] :=
Piecewise[{{2^(k/2) UE[m, 2^k t - 2 n + 1], (n - 1)/2^(k - 1) <= t <
n/2^(k - 1)}, {0, True}}];
PsiE[k_, M_, t_] :=
Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 2; M0 = 4; With[{k = k0, M = M0},
nn = Length[Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]];
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; ycol =
Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2,
nn + 1}]; tcol = ycol; Psijk =
With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 =
With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1]; Int3 = Integrate[Int2, t1]; Int4 =
Integrate[Int3, t1];
Psi[y_] := Psijk /. t1 -> y; int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y; int3[y_] := Int3 /. t1 -> y;
int4[y_] := Int4 /. t1 -> y;
wA = Table[wa[i][t], {i, nn}]; wB = Table[wb[i][t], {i, 4}];
w4[y_] := wA . Psi[y]; w3[y_] := wA . int1[y] + wB[[1]];
w2[y_] := wA . int2[y] + wB[[1]] y + wB[[2]];
w1[y_] := wA . int3[y] + wB[[1]] y^2/2 + wB[[2]] y + wB[[3]];
w0[y_] :=
wA . int4[y] + wB[[1]] y^3/6 + wB[[2]] y^2/2 + wB[[3]] y + wB[[4]];
tA = Table[ta[i][t], {i, nn}]; tB = Table[tb[i][t], {i, 2}];
T2[y_] := tA . Psi[y]; T1[y_] := tA . int1[y] + tB[[1]];
T0[y_] := tA . int2[y] + tB[[1]] y + tB[[2]];
eqw = With[{w = w0[y], T = T0[y]}, (D[w, t] == D[w, {y, 2}])];
eqnw = Table[eqw, {y, ycol}];
eqT = With[{w = w0[y],
T = T0[y]}, (D[T, t] == D[T, {y, 2}] + D[w, y]^2)];
eqnT = Table[eqT, {y, ycol}];
eqs = Join[eqnw, eqnT];
(*ic=With[{w=wvec.Psi[0],T=Tvec.Psi[0],P=Pvec.Psi[0]},{w==0,T==1,P==0}\
];*)
bc = With[{w = w0[y], T = T0[y]},
Join[{w == Cos[t], T == 1} /. y -> 0, {w == 0, T == 0} /.
y -> 1]];
icy = With[{w = w0[y], T = T0[y]}, {w == 0, T == 0} /. t -> 0]; ic =
Table[icy, {y, ycol}];
varAll = Join[wA, wB, tA, tB];
icn = Join[Flatten[ic], bc /. t -> 0]; eqn =
Join[eqs, D[bc, t]]; var1 = D[varAll, t];
{vec, mat} = CoefficientArrays[eqn, var1];
f = Inverse[mat // N] . (-vec);

sol2 = NDSolve[{Table[var1[[i]] == f[[i]], {i, Length[var1]}], icn}, 
   varAll, {t, 0, 10}];

@AlexTrounev CaputoD[w[y, t], {t, a}] == D[w[y, t], {y, 2}], CaputoD[T[y, t], {t, a}] == D[T[y, t], {y, 2}] + D[w[y, t], {y, 1}]^2 — zhk, Feb 06 '23 at 04:52
You use code to solve another system with 4-th order derivative. To solve your problem, please, see my answer. — Alex Trounev, Feb 07 '23 at 01:50

Alex Trounev · Accepted Answer · 2023-02-07T11:18:34.563

To solve this problem with predictor-corrector algorithm we need very small time step of about 10^-7, since transition zone is about 10^-6, see my answer here. To avoid this we can solve toy example with transition zone of about 1 as follows. 1. Solution at a=1:

eqns = {CaputoD[w[y, t], {t, a}] == D[w[y, t], {y, 2}], 
   CaputoD[T[y, t], {t, a}] == 
    D[T[y, t], {y, 2}] + D[w[y, t], {y, 1}]^2};
ics = {w[y, 0] == 0, T[y, 0] == 0};
bcs = {w[0, t] == (1 - Exp[-t]) Cos[t], T[0, t] == 1 - Exp[- t], 
  w[1, t] == 0, T[1, t] == 0}; var = {w, T}; sol1 = 
 NDSolveValue[{eqns, ics, bcs} /. a -> 1, var, {y, 0, 1}, {t, 0, 10}];
Table[Plot3D[sol1[[i]][y, t], {y, 0, 1}, {t, 0, 10}, 
  ColorFunction -> Hue, AxesLabel -> Automatic, 
  PlotLabel -> var[[i]]], {i, 2}]

Wavelets colocation method

UE[m_, t_] := EulerE[m, t];
psi[k_, n_, m_, t_] := 
  Piecewise[{{2^(k/2) UE[m, 2^k t - 2 n + 1], (n - 1)/2^(k - 1) <= t <
       n/2^(k - 1)}, {0, True}}];
PsiE[k_, M_, t_] := 
 Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 2; M0 = 4; With[{k = k0, M = M0}, 
 nn = Length[Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]];
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; ycol = 
 Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, 
   nn + 1}]; tcol = ycol; Psijk = 
 With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 = 
 With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1]; Int3 = Integrate[Int2, t1]; Int4 = 
 Integrate[Int3, t1];
Psi[y_] := Psijk /. t1 -> y; int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y;
wA = Table[wa[i][t], {i, nn}]; wB = Table[wb[i][t], {i, 2}];
w2[y_] := wA . Psi[y]; w1[y_] := wA . int1[y] + wB[[1]];
w0[y_] := wA . int2[y] + wB[[1]] y + wB[[2]];
tA = Table[ta[i][t], {i, nn}]; tB = Table[tb[i][t], {i, 2}];
T2[y_] := tA . Psi[y]; T1[y_] := tA . int1[y] + tB[[1]];
T0[y_] := tA . int2[y] + tB[[1]] y + tB[[2]];
eqw = With[{w = w0[y], T = T0[y]}, (D[w, t] == w2[y])];
eqnw = Table[eqw, {y, ycol}];
eqT = With[{w = w0[y], T = T0[y]}, (D[T, t] == T2[y] + w1[y]^2)];
eqnT = Table[eqT, {y, ycol}];
eqs = Join[eqnw, eqnT];
bc = With[{w = w0[y], T = T0[y]}, 
   Join[{w == (1 - Exp[-t]) Cos[t], T == 1 - Exp[-t]} /. 
     y -> 0, {w == 0, T == 0} /.
     y -> 1]];
icy = With[{w = w0[y], T = T0[y]}, {w == 0, T == 0} /. t -> 0]; ic = 
 Table[icy, {y, ycol}];
varAll = Join[wA, wB, tA, tB];
icn = Join[Flatten[ic], bc /. t -> 0]; eqn = 
 Join[eqs, D[bc, t]]; var1 = D[varAll, t];
{vec, mat} = CoefficientArrays[eqn, var1];
f = Inverse[mat // N] . (-vec);
sol2 = NDSolve[{Table[var1[[i]] == f[[i]], {i, Length[var1]}], icn}, 
   varAll, {t, 0, 10}];
{plw1 = Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 10}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "w"}], 
 plt1 = Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 10}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "T"}]};

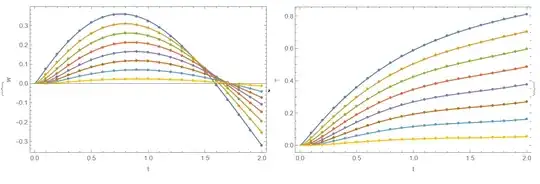
Visualization together with sol1 (red, dashed)

{Show[plw1, 
  Plot[Table[sol1[[1]][y, t], {y, ycol}], {t, 0, 10}, 
   PlotStyle -> {Red, Dashed}]], 
 Show[plt1, 
  Plot[Table[sol1[[2]][y, t], {y, ycol}], {t, 0, 10}, 
   PlotStyle -> {Red, Dashed}]]}

Predictor-corrector algorithm from the paper

vr0 = varAll /. t -> 0; {v0, mat0} = CoefficientArrays[icn, vr0];
s0 = Inverse[mat0] . (-v0);
rul0 = Table[vr0[[i]] -> s0[[i]], {i, Length[vr0]}];
f0 = f /. t -> 0 /. rul0;
[Alpha] = 1;
h = 10^-3; k1 = h^[Alpha]/Gamma[[Alpha] + 1]; k2 = 
 h^[Alpha]/Gamma[[Alpha] + 2]; nmax = 2000; m = Length[f]; For[
 k = 1, k <= nmax, k++, b[k] = k^[Alpha] - (k - 1)^[Alpha];
 a[k] = -(2k^([Alpha] + 1)) + (k - 1)^([Alpha] + 1) + (k + 
      1)^([Alpha] + 1); 
 c[k] = ((k - 1)^([Alpha] + 1) - (-[Alpha] + k - 1)
     k^[Alpha]);]; time = Table[j h, {j, 0, nmax + 1}];
Do[s[i, 0] = s0[[i]];, {i, 1, m}];
For[j = 1, j <= nmax, j++, 
   ff[j - 1] = 
    f /. Table[varAll[[ii]] -> s[ii, j - 1], {ii, m}] /. 
     t -> time[[j + 1]];
   Do[r[i, j] = (k1 Sum[b[j - th]ff[th][[i]], {th, 0, j - 1}]) + 
       s0[[i]];, {i, 1, m}];
   ff1[j] = (f /. Table[varAll[[ii]] -> r[ii, j], {ii, m}]) /. 
     t -> time[[j + 1]];
   Do[s[i, 
       j] = (k2 (Sum[a[j - tH]ff[tH][[i]], {tH, 1, j - 1}] + 
           ff1[j][[i]] + c[j]*f0[[i]])) + s0[[i]];, {i, 1, 
     m}];]; // AbsoluteTiming

It takes about 124s on my laptop. Visualization predictor-corrector solution (points) together with sol2

rule = Table[
    varAll[[i]] -> s[i, j] /. t -> time[[j + 1]], {i, m}, {j, 0, 
     nmax}] // Flatten;
lstT = Table[{time[[j]], T0[ycol[[i]]] /. t -> time[[j]]} /. rule, {i,
      nn}, {j, 100, nmax, 100}] // N;
lstw = Table[{time[[j]], w0[ycol[[i]]] /. t -> time[[j]]} /. rule, {i,
      nn}, {j, 100, nmax, 100}] // N;
{Show[Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 
    time[[nmax]]}, FrameLabel -> {"t", "w"}, PlotPoints -> 200, 
   Frame -> True], 
  ListPlot[lstw, PlotRange -> All, PlotStyle -> PointSize[.01]]], 
 Show[Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 
    time[[nmax]]}, FrameLabel -> {"t", "T"}, PlotPoints -> 200, 
   Frame -> True, PlotRange -> All], 
  ListPlot[lstT, PlotRange -> All, PlotStyle -> PointSize[.01]]]}

We also can integrate FDEs system CaputoD[varAll,{t,a}]==f with using Haar wavelets method. For this we map interval 0<=t<=tmax to the unit interval $0\le t \le 1$ and express CaputD in the Haar wavelets base as follows

tmax = 10;
UE[m_, t_] := EulerE[m, t];
psi[k_, n_, m_, t_] := 
  Piecewise[{{2^(k/2) UE[m, 2^k t - 2 n + 1], (n - 1)/2^(k - 1) <= t <
       n/2^(k - 1)}, {0, True}}];
PsiE[k_, M_, t_] := 
 Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 2; M0 = 4; With[{k = k0, M = M0}, 
 nn = Length[Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]];
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; ycol = 
 Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, nn + 1}]; Psijk = 
 With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 = 
 With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1]; Int3 = Integrate[Int2, t1]; Int4 = 
 Integrate[Int3, t1];
Psi[y_] := Psijk /. t1 -> y; int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y;
wA = Table[wa[i][t], {i, nn}]; wB = Table[wb[i][t], {i, 2}];
w2[y_] := wA . Psi[y]; w1[y_] := wA . int1[y] + wB[[1]];
w0[y_] := wA . int2[y] + wB[[1]] y + wB[[2]];
tA = Table[ta[i][t], {i, nn}]; tB = Table[tb[i][t], {i, 2}];
T2[y_] := tA . Psi[y]; T1[y_] := tA . int1[y] + tB[[1]];
T0[y_] := tA . int2[y] + tB[[1]] y + tB[[2]];
eqw = With[{w = w0[y], T = T0[y]}, (D[w, t]/tmax == w2[y])];
eqnw = Table[eqw, {y, ycol}];
eqT = With[{w = w0[y], 
    T = T0[y]}, (D[T, t]/tmax == T2[y] + w1[y]^2)];
eqnT = Table[eqT, {y, ycol}];
eqs = Join[eqnw, eqnT];
bc = With[{w = w0[y], T = T0[y]}, 
   Join[{w == (1 - Exp[-t tmax]) Cos[t tmax], T == 1 - Exp[-t tmax]} /. 
     y -> 0, {w == 0, T == 0} /.
     y -> 1]];
icy = With[{w = w0[y], T = T0[y]}, {w == 0, T == 0} /. t -> 0]; ic = 
 Table[icy, {y, ycol}];
varAll = Join[wA, wB, tA, tB];
icn = Join[Flatten[ic], bc /. t -> 0]; eqn = 
 Join[eqs, D[bc, t]]; var1 = D[varAll, t];
{vec, mat} = CoefficientArrays[eqn, var1];
f = Inverse[mat // N] . (-vec); vr0 = varAll /. t -> 0; {v0, mat0} = 
 CoefficientArrays[icn, vr0];
s0 = Inverse[mat0] . (-v0);
rul0 = Table[vr0[[i]] -> s0[[i]], {i, Length[vr0]}];
f0 = f /. t -> 0 /. rul0; m = Length[f]; sol2 = 
 NDSolve[{Table[var1[[i]] == f[[i]], {i, Length[var1]}], icn}, 
  varAll, {t, 0, 10}];
h[x_, k_, m_] := 
  WaveletPsi[HaarWavelet[], m x - k, WorkingPrecision -> Infinity];
p[x_, k_, m_] := 
  Piecewise[{{(1 + k - mx)/m, 
     k >= 0 && 1/m + (2k)/m - 2x < 0 && 1/m + k/m - x >= 0 && 
      m > 0}, {(-k + mx)/m, 
     k >= 0 && 1/m + (2k)/m - 2x >= 0 && k/m - x < 0 && 
      1/m + k/m - x >= 0 && m > 0}}, 0];
h1[x_] := WaveletPhi[HaarWavelet[], x, WorkingPrecision -> Infinity];
p1[x_] := Piecewise[{{1, x > 1}}, x];
pc[t_, k_, m_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     k == 0 && 1/m - 2t >= 0 && m > 0 && t > 0 && 
      1/m - t >= 
       0}, {-((m^(-1 + q)(1/(-k + mt))^(-1 + q))/(-1 + q)), 
     k > 0 && 1/m + (2k)/m - 2t > 0 && k/m - t < 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {(-t^q + 2mt^(1 + q) - 
        mt(-(1/(2m)) + t)^q)/(t^q(-(1/(2m)) + t)^q(m(-1 + q))),
      k == 0 && m > 0 && 1/m - 2t < 0 && 
      1/m - t >= 
       0}, {(1/(-1 + q))((2^(-1 + q)*
          m^(-1 + 2q)(-(-(k/m) + t)^q - 2k(-(k/m) + t)^q + 
            2mt(-(k/m) + t)^q + 2k(-((1/2 + k)/m) + t)^q - 
            2mt(-((1/2 + k)/m) + t)^q))/((1 + 2k - 2mt)(k - 
             mt))^q), 
     k > 0 && 1/m + (2k)/m - 2t == 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {-((1/(-1 + q))((2^(-1 + q)*
            m^(-1 + 2q)(-2(-((1/2 + k)/m) + t)^
                q((1 + 2k - 2mt)(k - mt))^q - 
              2k(-((1/2 + k)/m) + t)^
                q((1 + 2k - 2mt)(k - mt))^q + 
              2mt(-((1/2 + k)/m) + t)^
                q((1 + 2k - 2mt)(k - mt))^
                q + (-((1 + k)/m) + t)^
                q((1 + 2k - 2mt)(k - mt))^q + 
              2k(-((1 + k)/m) + t)^q((1 + 2k - 2mt)(k - mt))^
                q - 2mt(-((1 + k)/m) + t)^
                q((1 + 2k - 2mt)(k - mt))^q + (-(k/m) + t)^
                q((1 + 2k - 2mt)(1 + k - mt))^q + 
              2k(-(k/m) + t)^q((1 + 2k - 2mt)(1 + k - mt))^
                q - 2mt(-(k/m) + t)^
                q((1 + 2k - 2mt)(1 + k - mt))^q - 
              2k(-((1/2 + k)/m) + t)^
                q((1 + 2k - 2mt)(1 + k - mt))^q + 
              2mt(-((1/2 + k)/m) + t)^
                q((1 + 2k - 2mt)(1 + k - mt))^
                q))/(((1 + 2k - 2mt)(k - mt))^
             q((1 + 2k - 2mt)(1 + k - mt))^q))), 
     k > 0 && m > 0 && 1/m + (2k)/m - 2t <= 0 && 
      1/m + k/m - t <= 
       0}, {-((1/(2*
            m(-1 + q)))((2^qm^(2q)*
             t^q(-(1/m) + t)^q(-(1/(2m)) + t)^q - 
            2^(1 + q)m^(1 + 2q)
             t^(1 + q)(-(1/m) + t)^q(-(1/(2m)) + t)^q - 
            2^(1 + q)m^(2q)t^q(-(1/(2m)) + t)^(2q) + 
            2^(1 + q)m^(1 + 2q)t^(1 + q)(-(1/(2m)) + t)^(2q) + 
            t^q((-1 + mt)(-1 + 2mt))^q - 
            2mt^(1 + q)((-1 + mt)(-1 + 2mt))^q + 
            2mt(-(1/(2m)) + t)^q((-1 + mt)(-1 + 2mt))^q)/(t^
             q(-(1/(2m)) + t)^q((-1 + mt)(-1 + 2mt))^q))), 
     k == 0 && 1/m - 2t < 0 && 1/m - t < 0 && 
      m > 0}, {(1/(-1 + q))((2^(-1 + q)
          m^(-1 + q)((-m^q)(-(k/m) + t)^q - 
            2km^q(-(k/m) + t)^q + 2m^(1 + q)t(-(k/m) + t)^q + 
            2km^q(-((1/2 + k)/m) + t)^q - 
            2m^(1 + q)*
             t(-((1/2 + k)/m) + t)^q - ((1 + 2k - 2mt)(k - mt))^
              q(1/(-1 - 2k + 2mt))^q - 
            2k((1 + 2k - 2mt)(k - mt))^
              q(1/(-1 - 2k + 2mt))^q + 
            2mt((1 + 2k - 2mt)(k - mt))^
              q(1/(-1 - 2k + 2mt))^q))/((1 + 2k - 2mt)(k - 
             mt))^q), 
     1/m + (2k)/m - 2t < 0 && k > 0 && m > 0 && 1/m + k/m - t > 0}},
    0];
pc1[t_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     t <= 1}}, -(((-1 + t)^qt + t^q - t^(1 + q))/((-1 + t)^q
        t^q*(-1 + q)))];
q = 8/10; tn = 1/tmax^q/Gamma[1 - q];
J = 5; M = 2^J;
dt = 1/(2*M); tl = Table[l dt, {l, 0, 2 M}];
Tcol = Table[(tl[[l - 1]] + tl[[l]])/2, {l, 2, 2 M + 1}];
U1[k_][t_, q_] := 
  Sum[v[k][i, j] pc[t, i, 2^j, q], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] +
    v1[k] pc1[t, q];
U0[k_][t_] := 
  Sum[v[k][i, j] p[t, i, 2^j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   v1 [k] p1[t] + v2[k];
varM = Join[Flatten[Table[{v2[k], v1[k]}, {k, m}]], 
  Flatten[Table[
    v[k][i, j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}, {k, m}]]]; rult = 
 Table[varAll[[k]] -> U0[k][t], {k, m}];
eq[q_] := 
 Flatten[Table[
   U1[k][t, q] tn == f[[k]]/tmax /. rult, {t, Tcol}, {k, m}]]; ict = 
 Table[U0[k][0] == s0[[k]], {k, m}];
sol = FindRoot[Join[eq[q], ict], 
   Table[{varM[[i]], 1/10}, {i, Length[varM]}]];

Visualization NDSolve solution at a=1

{plw1 = Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "w"}, 
   PlotStyle -> Dashed], 
 plt1 = Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "T"}, 
   PlotStyle -> Dashed]}

FDEs system solution at a=4/5

{plw2 = Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. rult /. sol], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "w"}], 
 plt2 = Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. rult /. sol], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "T"}]}

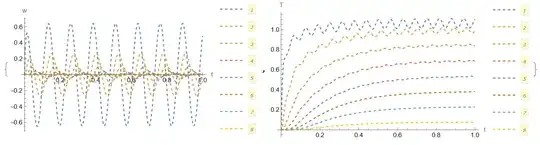
Solution with a=1 (dashed lines) and a=4/5 (solid lines)

{Show[plw1, plw2], Show[plt1, plt2]}

Update 1. For any space range [0, L] and time range [0, tmax] we need to map solution on [0, 1] to solve the problem with wavelets defined on the unit interval. For diffusion equation $w_t=w_{yy}$ after rescaling we have $w_t=df w_{yy}$ where the effective diffusion parameter is $df=tmax/L^2$. For example,

L = 10; tmax = 50; df = tmax/L^2;
UE[m_, t_] := EulerE[m, t];
psi[k_, n_, m_, t_] := 
  Piecewise[{{2^(k/2) UE[m, 2^k t - 2 n + 1], (n - 1)/2^(k - 1) <= t <
       n/2^(k - 1)}, {0, True}}];
PsiE[k_, M_, t_] := 
 Flatten[Table[psi[k, n, m, t], {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]
k0 = 2; M0 = 4; With[{k = k0, M = M0}, 
 nn = Length[Flatten[Table[1, {n, 1, 2^(k - 1)}, {m, 0, M - 1}]]]];
dx = 1/(nn); xl = Table[l*dx, {l, 0, nn}]; ycol = 
 Table[(xl[[l - 1]] + xl[[l]])/2, {l, 2, nn + 1}]; Psijk = 
 With[{k = k0, M = M0}, PsiE[k, M, t1]]; Int1 = 
 With[{k = k0, M = M0}, Integrate[PsiE[k, M, t1], t1]];
Int2 = Integrate[Int1, t1]; Int3 = Integrate[Int2, t1]; Int4 = 
 Integrate[Int3, t1];
Psi[y_] := Psijk /. t1 -> y; int1[y_] := Int1 /. t1 -> y;
int2[y_] := Int2 /. t1 -> y;
wA = Table[wa[i][t], {i, nn}]; wB = Table[wb[i][t], {i, 2}];
w2[y_] := wA . Psi[y]; w1[y_] := wA . int1[y] + wB[[1]];
w0[y_] := wA . int2[y] + wB[[1]] y + wB[[2]];
tA = Table[ta[i][t], {i, nn}]; tB = Table[tb[i][t], {i, 2}];
T2[y_] := tA . Psi[y]; T1[y_] := tA . int1[y] + tB[[1]];
T0[y_] := tA . int2[y] + tB[[1]] y + tB[[2]];
eqw = With[{w = w0[y], T = T0[y]}, (D[w, t] == df w2[y])];
eqnw = Table[eqw, {y, ycol}];
eqT = With[{w = w0[y], 
    T = T0[y]}, (D[T, t] == df (T2[y] + w1[y]^2))];
eqnT = Table[eqT, {y, ycol}];
eqs = Join[eqnw, eqnT];
(ic=With[{w=wvec.Psi[0],T=Tvec.Psi[0],P=Pvec.Psi[0]},{w==0,T==1,P==0}

];)
bc = With[{w = w0[y], T = T0[y]}, 
   Join[{w == Cos[t tmax], T == 1} /. y -> 0, {w == 0, T == 0} /.
     y -> 1]];
icy = With[{w = w0[y], T = T0[y]}, {w == 0, T == 0} /. t -> 0]; ic = 
 Table[icy, {y, ycol}];
varAll = Join[wA, wB, tA, tB];
icn = Join[Flatten[ic], bc /. t -> 0]; eqn = 
 Join[eqs, D[bc, t]]; var1 = D[varAll, t];
{vec, mat} = CoefficientArrays[eqn, var1];
f = Inverse[mat // N] . (-vec); vr0 = varAll /. t -> 0; {v0, mat0} = 
 CoefficientArrays[icn, vr0];
s0 = Inverse[mat0] . (-v0);
rul0 = Table[vr0[[i]] -> s0[[i]], {i, Length[vr0]}];
f0 = f /. t -> 0 /. rul0; m = Length[f]; sol2 = 
 NDSolve[{Table[var1[[i]] == f[[i]], {i, Length[var1]}], icn}, 
  varAll, {t, 0, 1}];

Visualization solution sol2 computed at a=1

{plw1 = Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "w"}, 
   PlotStyle -> Dashed, PlotRange -> All], 
 plt1 = Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. sol2[[1]]], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "T"}, 
   PlotStyle -> Dashed]}

h[x_, k_, m_] := 
  WaveletPsi[HaarWavelet[], m x - k, WorkingPrecision -> Infinity];
p[x_, k_, m_] := 
  Piecewise[{{(1 + k - m*x)/m, 
     k >= 0 && 1/m + (2*k)/m - 2*x < 0 && 1/m + k/m - x >= 0 && 
      m > 0}, {(-k + m*x)/m, 
     k >= 0 && 1/m + (2*k)/m - 2*x >= 0 && k/m - x < 0 && 
      1/m + k/m - x >= 0 && m > 0}}, 0];
h1[x_] := WaveletPhi[HaarWavelet[], x, WorkingPrecision -> Infinity];
p1[x_] := Piecewise[{{1, x > 1}}, x];
pc[t_, k_, m_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     k == 0 && 1/m - 2*t >= 0 && m > 0 && t > 0 && 
      1/m - t >= 
       0}, {-((m^(-1 + q)*(1/(-k + m*t))^(-1 + q))/(-1 + q)), 
     k > 0 && 1/m + (2*k)/m - 2*t > 0 && k/m - t < 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {(-t^q + 2*m*t^(1 + q) - 
        m*t*(-(1/(2*m)) + t)^q)/(t^q*(-(1/(2*m)) + t)^q*(m*(-1 + q))),
      k == 0 && m > 0 && 1/m - 2*t < 0 && 
      1/m - t >= 
       0}, {(1/(-1 + q))*((2^(-1 + q)*
          m^(-1 + 2*q)*(-(-(k/m) + t)^q - 2*k*(-(k/m) + t)^q + 
            2*m*t*(-(k/m) + t)^q + 2*k*(-((1/2 + k)/m) + t)^q - 
            2*m*t*(-((1/2 + k)/m) + t)^q))/((1 + 2*k - 2*m*t)*(k - 
             m*t))^q), 
     k > 0 && 1/m + (2*k)/m - 2*t == 0 && m > 0 && 
      1/m + k/m - t > 
       0}, {-((1/(-1 + q))*((2^(-1 + q)*
            m^(-1 + 2*q)*(-2*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q - 
              2*k*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + 
              2*m*t*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^
                q + (-((1 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + 
              2*k*(-((1 + k)/m) + t)^q*((1 + 2*k - 2*m*t)*(k - m*t))^
                q - 2*m*t*(-((1 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(k - m*t))^q + (-(k/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q + 
              2*k*(-(k/m) + t)^q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^
                q - 2*m*t*(-(k/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q - 
              2*k*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q + 
              2*m*t*(-((1/2 + k)/m) + t)^
                q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^
                q))/(((1 + 2*k - 2*m*t)*(k - m*t))^
             q*((1 + 2*k - 2*m*t)*(1 + k - m*t))^q))), 
     k > 0 && m > 0 && 1/m + (2*k)/m - 2*t <= 0 && 
      1/m + k/m - t <= 
       0}, {-((1/(2*
            m*(-1 + q)))*((2^q*m^(2*q)*
             t^q*(-(1/m) + t)^q*(-(1/(2*m)) + t)^q - 
            2^(1 + q)*m^(1 + 2*q)*
             t^(1 + q)*(-(1/m) + t)^q*(-(1/(2*m)) + t)^q - 
            2^(1 + q)*m^(2*q)*t^q*(-(1/(2*m)) + t)^(2*q) + 
            2^(1 + q)*m^(1 + 2*q)*t^(1 + q)*(-(1/(2*m)) + t)^(2*q) + 
            t^q*((-1 + m*t)*(-1 + 2*m*t))^q - 
            2*m*t^(1 + q)*((-1 + m*t)*(-1 + 2*m*t))^q + 
            2*m*t*(-(1/(2*m)) + t)^q*((-1 + m*t)*(-1 + 2*m*t))^q)/(t^
             q*(-(1/(2*m)) + t)^q*((-1 + m*t)*(-1 + 2*m*t))^q))), 
     k == 0 && 1/m - 2*t < 0 && 1/m - t < 0 && 
      m > 0}, {(1/(-1 + q))*((2^(-1 + q)*
          m^(-1 + q)*((-m^q)*(-(k/m) + t)^q - 
            2*k*m^q*(-(k/m) + t)^q + 2*m^(1 + q)*t*(-(k/m) + t)^q + 
            2*k*m^q*(-((1/2 + k)/m) + t)^q - 
            2*m^(1 + q)*
             t*(-((1/2 + k)/m) + t)^q - ((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q - 
            2*k*((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q + 
            2*m*t*((1 + 2*k - 2*m*t)*(k - m*t))^
              q*(1/(-1 - 2*k + 2*m*t))^q))/((1 + 2*k - 2*m*t)*(k - 
             m*t))^q), 
     1/m + (2*k)/m - 2*t < 0 && k > 0 && m > 0 && 1/m + k/m - t > 0}},
    0];
pc1[t_, q_] := 
  Piecewise[{{-(t^(1 - q)/(-1 + q)), 
     t <= 1}}, -(((-1 + t)^q*t + t^q - t^(1 + q))/((-1 + t)^q*
        t^q*(-1 + q)))];
q = 90/100; tn = 1/tmax^q/Gamma[1 - q];
J = 6; M = 2^J;
dt = 1/(2*M); tl = Table[l dt, {l, 0, 2 M}];
Tcol = Table[(tl[[l - 1]] + tl[[l]])/2, {l, 2, 2 M + 1}];
U1[k_][t_, q_] := 
  Sum[v[k][i, j] pc[t, i, 2^j, q], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] +
    v1[k] pc1[t, q];
U0[k_][t_] := 
  Sum[v[k][i, j] p[t, i, 2^j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}] + 
   v1 [k] p1[t] + v2[k];
varM = Join[Flatten[Table[{v2[k], v1[k]}, {k, m}]], 
  Flatten[Table[
    v[k][i, j], {j, 0, J, 1}, {i, 0, 2^j - 1, 1}, {k, m}]]]; rult = 
 Table[varAll[[k]] -> U0[k][t], {k, m}];
eq[q_] := 
 Flatten[Table[
   U1[k][t, q] tn == f[[k]]/tmax /. rult, {t, Tcol}, {k, m}]]; ict = 
 Table[U0[k][0] == s0[[k]], {k, m}];
sol = FindRoot[Join[eq[q], ict], 
   Table[{varM[[i]], 1/10}, {i, Length[varM]}]];

Visualization solution at a=0.9

{plw2 = Plot[
   Evaluate[Table[w0[y], {y, ycol}] /. rult /. sol], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "w"}, 
   PlotRange -> All], 
 plt2 = Plot[
   Evaluate[Table[T0[y], {y, ycol}] /. rult /. sol], {t, 0, 1}, 
   PlotLegends -> Automatic, AxesLabel -> {"t", "T"}]}

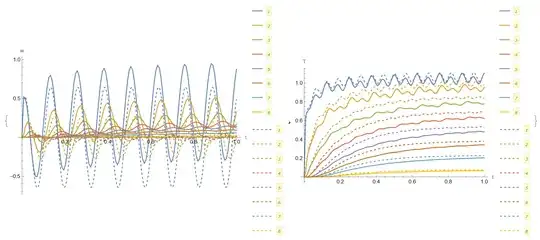
Note, that in the last case we don't use Exp[- t tmax] to compute transition zone. Visualization solution at a=1 (dashed lines) and at a=0.9 (solid lines)

@zhk This is effect from w oscillation since T depends on $w_y^2$ as it states in your equation CaputoD[T[y, t], {t, a}] == D[T[y, t], {y, 2}] + D[w[y, t], {y, 1}]^2. — Alex Trounev, Feb 07 '23 at 03:28
How to extend the range for y to [0,10] and plotT vs y`? — zhk, Feb 07 '23 at 07:22

Error in Euler wavelets collocation method

1 Answers1