How to get the normal vector of a planar curve pointing "outside" (its circle of curvature)?

Question

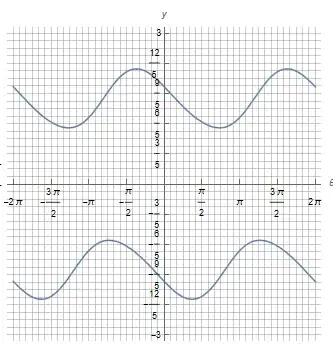
I have the following implicit function, for which I need to pick up a point $(x0, y0)$ on it and determine the expression of its normal vector pointing outside. "Outside" here means that the said vector points towards the opposite side of the circle of curvature.

-2.75 + y^2 - Cos[x] + y Sin[x]==0

Its figure looks like:

To see the essence of my question, we can look at a simpler example:

Let's say we have a planar curve $x^2+y^2=1$, upon differentiation, we obtain $(2x,2y)\cdot (dx, dy)=0$, with $(dx, dy)$ associated with the tangent direction of the curve at point $(x,y)$. Hence, $(2x,2y)$ is parallel to the normal vector.

My question is, how to decide whether $(2x,2y)$ or $-(2x,2y)$ points outside the curve, and how to implement this in Mathematica?

Update 1:

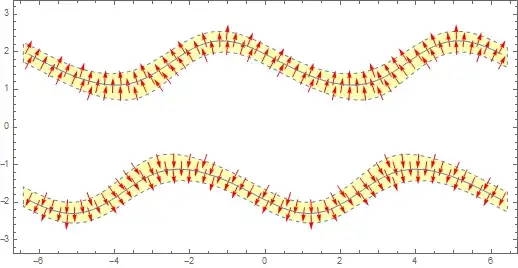
My previous statement may be ambiguous; I'm not trying to get the normal vectors pointing outside sth, which seems to be what @Syed has produced. The precise statement should be that, if we place the end of the arrow of the normal vector on the curve, then its head should be pointing in the direction opposite to the circle of curvature.

Taking the cosine function as an example, the arrows between $0,\pi/2$ should be pointing right up, while those between $\pi/2,0$ should be pointing left down. In other words, I want to know which side the curve lies w.r.t. the tangent line.

This is more general but in a special case simply answers the question: Finding unit tangent, normal, and binormal vectors for a given r(t) — Artes, Feb 13 '23 at 02:23

score 2 · Answer 1 · answered Feb 12 '23 at 17:44

The function "FrenetSerretSystem" will give you the signed curvature, the tangent vector and the normal vector of a parametrized curve. Therefore to use it, we must first get a parametrized curve, I choose arbitrarily "x" as a parameter. To keep things simple, I only do it for the lower of the 2 branches:

Clear["Globals`*"];
impl = -2.75 + y^2 - Cos[x] + y Sin[x] == 0;
curve[x_] = {x, y} /. Solve[impl, y][[1]];
sol[x_] = FrenetSerretSystem[curve[x], x];

Now "sol" contains everything we need to draw a graphics:

Manipulate[
 pos = param[x][[1]];
 {{dir}, {tan, nor}} = sol[x];
 Show[
  Graphics[{ Arrow[{{pos, pos + tan}}] , 
    Arrow[{{pos, pos - Sign[dir] nor}}]
    }, PlotRange -> {6.6 {-1, 1}, {-3, 3}}, AxesLabel -> {"X", "Y"}, 
   Axes -> True
   ], background]
 , {x, -2 Pi, 2 Pi}

]

thanks, I'll look into this solution, and it would be good if I can display a series of arrows similar to @Syed produced. I'll try. — larry, Feb 12 '23 at 19:12

score 1 · Answer 2 · answered Feb 12 '23 at 17:27

Using VectorPlot:

eq2 = -2.75 + y^2 - Cos[x] + y Sin[x] == 0
First@D[eq2, #] & /@ {x, y}

{y Cos[x] + Sin[x], 2 y + Sin[x]}

Show[VectorPlot[{y Cos[x] + Sin[x], 2 y + Sin[x]}
  , {x, -2 π, 2 π}, {y, -π, π}
  , ClippingStyle -> None
  , MaxRecursion -> 2
  , VectorColorFunction -> None
  , VectorStyle -> Red
  , VectorSizes -> 1.4
  , VectorPoints -> {32}
  , RegionFunction -> 
   Function[{x, y}, -1 < -2.75 + y^2 - Cos[x] + y Sin[x] < 1]
  , RegionFillingStyle -> Yellow
  , RegionBoundaryStyle -> Dashed
  , AspectRatio -> Automatic
  , ImageSize -> Large
  ]
 , ContourPlot[
  Evaluate@eq2, {x, -2 π, 2 π}, {y, -π, π}]
 ]

To flip the sign of the vectors, use a negative sign in one of the entries.

How to get the normal vector of a planar curve pointing "outside" (its circle of curvature)?

2 Answers2