How to use MMA to solve the minimal surface?

Question

There is a great old post, but since MMA greatly improves the ability of solving differential equations, especially the Region can be used to define the range of variables. So I ask it again. As the Lagrange's Equation: $$(1+f_y^2)f_{xx}+(1+f_x^2)f_{yy}=2f_xf_yf_{xy}$$So we can make expression in MMA:

NDSolve[{(1+D[u[x,y],y]^2)D[u[x,y],{x,2}]+(1+D[u[x,y],x]^2)D[u[x,y],{y,2}]==2D[u[x,y],x]D[u[x,y],y]D[u[x,y],x,y],
DirichletCondition[u[x,y]==2,x^2+y^2==4 Cosh[1]^2],
DirichletCondition[u[x,y]==-2,x^2+y^2==4 Cosh[1]^2]},u[x,y],{x,-2,2},{y,-2,2}]

But it doesn't look like MMA can solve this differential equation. Did I make a mistake? I don't want to get the exact solution, I just want to get the numerical solution and plot it.

---

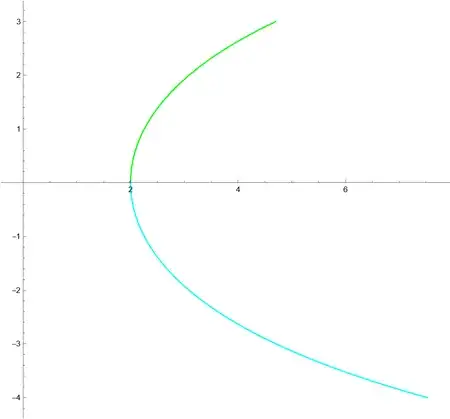
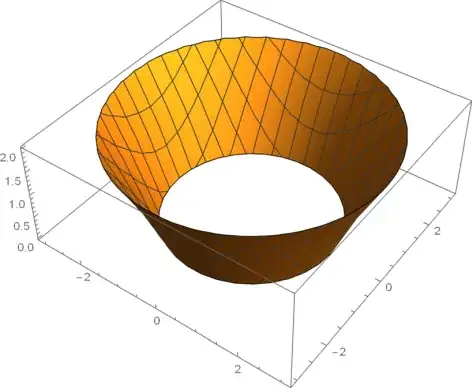
I actually know the solution of this differential equation, and I can plot it with this code:

a=2;
RevolutionPlot3D[{a*Cosh[z/a],z},{z,-2,2}]

Answer 1

• Since the Lagrange's Equation only work for the surfaces as graphs of functions,that is,the surface must be the form of {x,y,f[x,y]} and {x, y} ∈ 2D region,so it doesn't work for general parametric surfaces.

• Here we seperate the parametric surface to two graphs of functions and using the divergence form of the Lagrange's Equation respectly.

a = 2;
h1 = 3;
h2 = 4;
catenary[z_] = a*Cosh[z/a];
ParametricPlot[{catenary[z], z}, {z, -h2, h1}, AxesOrigin -> {0, 0}, 
 MeshFunctions -> {#2 &}, Mesh -> {{0}}, MeshShading -> {Cyan, Green}]

• Divergence form of the Lagrange's Equation for two graphs.

Clear["Global`*"];
a = 2;
h1 = 3;
h2 = 4;
catenary[z_] = a*Cosh[z/a];
reg1 = Annulus[{0, 0}, {catenary[0], catenary[h1]}];
reg2 = Annulus[{0, 0}, {catenary[0], catenary[h2]}];
sol1 = NDSolve[{Inactive[Div][Grad[u[x, y], {x, y}]/Sqrt[
      1 + Grad[u[x, y], {x, y}] . Grad[u[x, y], {x, y}]], {x, y}] == 
     0, {DirichletCondition[u[x, y] == 0, x^2 + y^2 == catenary[0]^2],
      DirichletCondition[u[x, y] == h1, 
      x^2 + y^2 == catenary[h1]^2]}}, u[x, y], {x, y} ∈ reg1];
sol2 = NDSolve[{Inactive[Div][Grad[u[x, y], {x, y}]/Sqrt[
      1 + Grad[u[x, y], {x, y}] . Grad[u[x, y], {x, y}]], {x, y}] == 
     0, {DirichletCondition[u[x, y] == 0, x^2 + y^2 == catenary[0]^2],
      DirichletCondition[u[x, y] == -h2, 
      x^2 + y^2 == catenary[h2]^2]}}, u[x, y], {x, y} ∈ reg2];
graphs = {Plot3D[u[x, y] /. sol1, {x, y} ∈ reg1, 
   PlotStyle -> Green, Mesh -> None, PlotRange -> All], 
  Plot3D[u[x, y] /. sol2, {x, y} ∈ reg2, PlotStyle -> Cyan, 
   Mesh -> None, PlotRange -> All], 
  RevolutionPlot3D[{a*Cosh[z/a], z}, {z, -h2, h1}]}
Show[graphs, PlotRange -> All]

Answer 2

The pde might be rewritten as first order pde with inactive parts:

pde= (1 + D[z[x, y], y]^2) D[z[x, y], {x, 2}] + (1 + D[z[x, y], x]^2) D[z[x, y], {y, 2}] -2 D[z[x, y], x] D[z[x, y], y] D[z[x, y], x, y]

first order form:

    Div[ {Derivative[1, 0][z][x, y], Derivative[0, 1 ][z][x, y]}, {x, 
     y}] + Derivative[1, 0][z][x, 
     y] Grad[Derivative[0, 1 ][z][x, y], {x, y}] . 
     Cross[{Derivative[1, 0][z][x, y], Derivative[0, 1 ][z][x, y]}] - 
   Derivative[0, 1 ][z][x, 
     y] Grad[Derivative[1, 0  ][z][x, y], {x, y}] . 
     Cross[{Derivative[1, 0  ][z][x, y], 
       Derivative[0, 1 ][z][x, y]}] == pde  // Simplify (*True*)

With modiffied dirichlet conditions Mathematica is able to solve the problem in the region reg

reg = Annulus[{0, 0}, {2 Cosh[0], 2 Cosh[1] }]
Z = NDSolveValue[{Inactive[Div][ {Derivative[1, 0][z][x, y], 
       Derivative[0, 1 ][z][x, y]}, {x, y}] + 
     Derivative[1, 0][z][x, 
       y] Inactive[Grad][Derivative[0, 1 ][z][x, y], {x, y}] . 
       Inactive[
        Cross[{Derivative[1, 0][z][x, y], 
          Derivative[0, 1 ][z][x, y]}]] - 
     Derivative[0, 1 ][z][x, 
       y] Inactive[Grad][Derivative[1, 0  ][z][x, y], {x, y}] . 
       Inactive[
        Cross[{Derivative[1, 0  ][z][x, y], 
          Derivative[0, 1 ][z][x, y]}]] == 0, 
   DirichletCondition[z[x, y] == 2, x^2 + y^2 == (2 Cosh[1])^2], 
   DirichletCondition[z[x, y] == 0, x^2 + y^2 == (2  Cosh[0])^2]}, z ,
   Element[{x, y}, reg]]
Plot3D[Z[x, y], Element[{x, y}, reg]]

I don't know why solution plot differs from your revolutionplot.

Hope it helps!