How can I obtain the closed-form description of the particle path? (If possible...)

Question

With respect to the following image 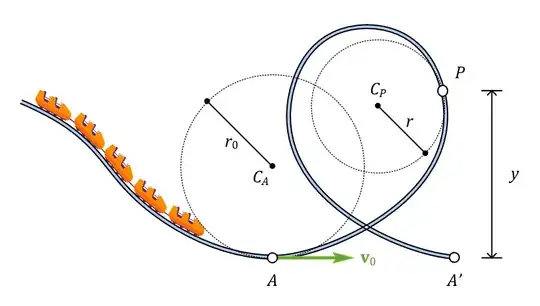, the rollercoaster track between points A and A' is such so that the centripetal force is constant, corresponding to its initial value at point A: an=v0^2/r0, where r0 is the radius of the initial curvature and v0 the velocity at point A. It turns out that the radius of curvature at an arbitrary point P of the track is given as r=r0(1-2gy/vo^2), i.e. it is a function of the height y. I can evaluate the track incrementally, where the coordinates of point A is 0,0 for convenience, as: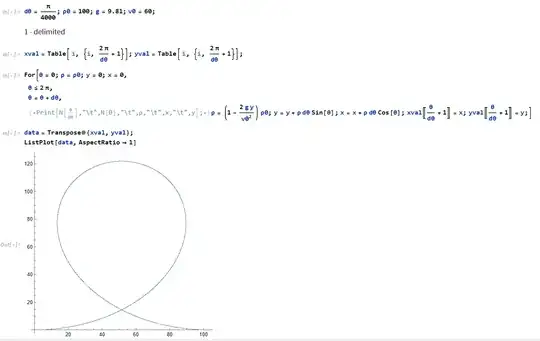

Is there a way to evaluate a closed-form solution for the track? I tried the following:

FullSimplify[
 RSolveValue[
  y[k] == y[k - 1] + (1 - (2 g y[k - 1])/v0^2) r0 dθ Sin[k dθ], 
  y[k], k]]

But no solution comes out. What I need is the limit of the above expression when dθ->0, in closed form. I hope the description if sufficient. Any ideas?

Answer 1

I solved this by writing dy = r0 (1 - (2 g y)/v0^2) Sin[θ]dθ, so the result can be obtained by integration. The maximum height is evaluated by:

{ymax} = 
 SolveValues[
   Integrate[1/(r0 (1 - (2 g y)/v0^2)), {y, 0, ymax}] == 
    Integrate[Sin[θ], {θ, 0, π}], ymax] // FullSimplify
{((1 - E^(-((4 g r0)/v0^2))) v0^2)/(2 g)}