Plotting a tangent to a parametric space curve(3D) at a certain point

Question

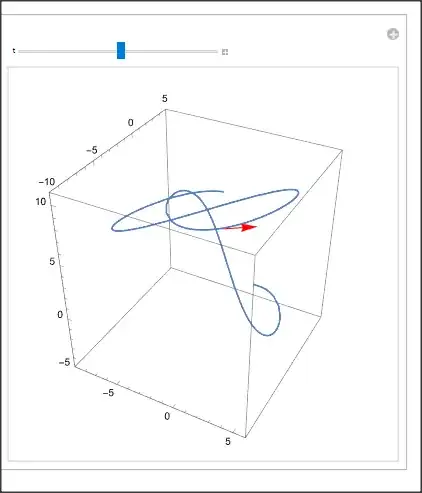
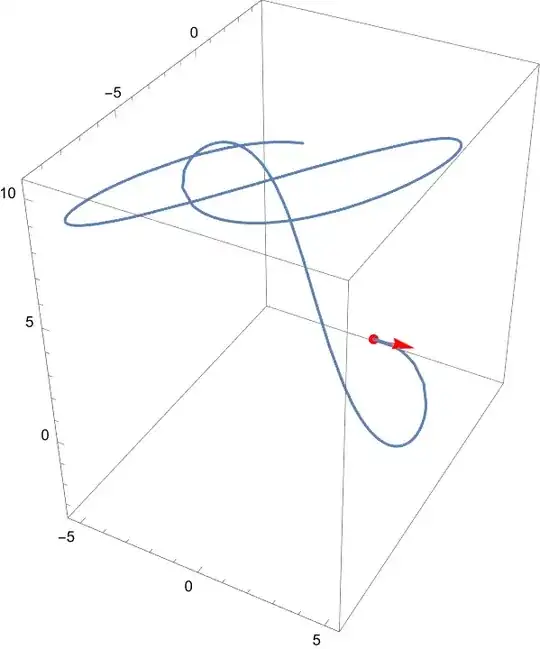
So I have this curve:

r[t_] := {5 Sin[2 t], -t + 4 Cos[3 t], (2 t - 3 Cos[t])}

I am trying to plot a tangent to this curve at t=2. When I try to do the following:

tangent = ParametricPlot3D[r'[t], {t, -5, 5}]

It gives me nothing or just a single point. Am I doing it wrong and if so what's the right way to do it?

score 7 · Accepted Answer · answered Feb 17 '23 at 09:39

7

A tangent is defined by: start point: r[t] and end point: r[t]+r'[t]. E.g.(the length of the tangent is scaled):

r[t_] = {5 Sin[2 t], -t + 4 Cos[3 t], (2 t - 3 Cos[t])};
bg = ParametricPlot3D[r[t], {t, 0, 2 Pi}];
Manipulate[
 Show[Graphics3D[{
    Red, Arrow[{r[t], (r[t] + 0.3 r'[t])}]
    }, Axes -> True, PlotRange -> {{-9, 6}, {-10, 5}, {-5, 11}}], bg]
 , {t, 0, 2 Pi}]

answered Feb 17 '23 at 09:39

Daniel Huber

51,463
1
23
57

Simplest and best approach: +1 for specific question. FrenetSerretSystem (overkill by me)…normal and binormal nice bonus but unnecessary for question posed. – ubpdqn Feb 17 '23 at 10:14

score 6 · Answer 2 · answered Feb 17 '23 at 07:24

You can use FrenetSerretSystem

For example:

r[t_] := {5 Sin[2 t], -t + 4 Cos[3 t], (2 t - 3 Cos[t])}
tg[u_, s_] := 
 Arrow[{r[u], 
   r[u] + s (FrenetSerretSystem[r[t], t][[2, 1]]) /. t -> u}]
Manipulate[
 Show[ParametricPlot3D[r[t], {t, 0, 2 Pi}], 
  Graphics3D[{Red, PointSize[0.02], Point[r[p]], tg[p, 2]}]], {p, 0, 
  2 Pi}]

Plotting a tangent to a parametric space curve(3D) at a certain point

2 Answers2