What do the arguments of a generated BSplineFunction mean?

Question

For example, if we evaluate this:

BSplineFunction@{{0,100},{200,50},{200,0}}

we'll get

BSplineFunction[1,
    {{0., 1.}},
    {2}, {False}, {{{0., 100.}, {200., 50.}, {200., 0.}}, Automatic},
    {{0., 0., 0., 1., 1., 1.}},
    {0}, MachinePrecision, "Unevaluated"
]

What do these mean?

Answer 1

Mimicking the spelunking in

How to splice together several instances of InterpolatingFunction?

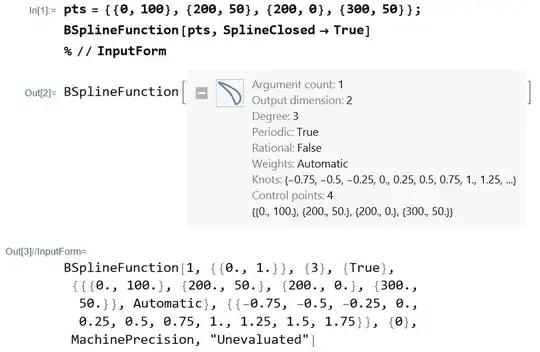
We find

func = BSplineFunction[{{0, 100}, {200, 50}, {200, 0}, {300, 0}}];
lst = func@Methods
(* {"Closed", "ControlPoints", "Degree", "DerivativeOrder", "Domain", 
    "Evaluate", "ExtrapolationMethod", "Knots", "MethodInformation", 
    "Methods", "Properties", "Rank", "Weights", "WorkingPrecision"} *)
func@MethodInformation@# & /@ lst;

System`BSplineFunction`Closed

BSplineFunction[domain, data]@Closed[] returns the closedness of the B-spline function in each dimension.

System`BSplineFunction`ControlPoints

BSplineFunction[domain, data]@ControlPoints gives the control points.

System`BSplineFunction`Degree

BSplineFunction[domain, data]@Degree[] returns the polynomial degree of the B-spline function in each dimension.

System`BSplineFunction`DerivativeOrder

BSplineFunction[domain, data]@DerivativeOrder[] returns what derivative of the B-spline function will be computed upon evaluation.

System`BSplineFunction`Domain

BSplineFunction[domain, data]@Domain[] returns the domain inteval in each direction.

System`BSplineFunction`Evaluate

BSplineFunction[domain, data]@Evaluate[arg] evaluates the B-spline function at the argument arg.

System`BSplineFunction`ExtrapolationMethod

BSplineFunction[domain, data]@ExtrapolationMethod returns what type of extrapolation method will be used upon evaulation outside the domain.

System`BSplineFunction`Knots

BSplineFunction[domain, data]@Knots[] returns the knot sequence in each dimension.

System`BSplineFunction`MethodInformation

BSplineFunction[domain, data]@MethodInformation[method] gives information about a particular method.

System`BSplineFunction`Methods

BSplineFunction[domain, data]@Methods[pat] gives the list of methods matching the string pattern pat.

System`BSplineFunction`Properties

BSplineFunction[domain, data]@Properties gives the list of possible properties.

System`BSplineFunction`Rank

BSplineFunction[domain, data]@Rank gives the rank of the B-spline function domain.

System`BSplineFunction`Weights

BSplineFunction[domain, data]@Weights gives the weights associated with the control points.

System`BSplineFunction`WorkingPrecision

BSplineFunction[domain, data]@WorkingPrecision returns what working precision will be used during the computation.

It's worth pointing out that, the ExtrapolationMethod method doesn't have any effect at least in v13.2.

With these info, I can figure out the meaning of Most of the arguments:

BSplineFunction[Rank, Domain, Degree, Closed, 
                {ControlPoints, Weights}, Knots, DerivativeOrder, 
                WorkingPrecision, ???]

Yeah, I don't know what "Unevaluated" means. Seems that even if it's changed to anything else, it'll simply be ignored. (If I have to guess, it might be a position for the unfinished ExtrapolationMethod? )

BTW, it's worth mentioning that, even if the Domain is changed to anything else, it's simply ignored. I guess there're more, but it's time to go to bed now.

Answer 2

This is the full internal representation of BSplineFunction with all relevant parameters. You can fiddle around with the options, then open the information box and compare the values to find the correspondence.

pts = {{0, 100}, {200, 50}, {200, 0}, {300, 50}};
BSplineFunction[pts, SplineClosed -> True]
% // InputForm

The syntax is therefore:

BSplineFunction[Rank, ?, SplineDegree, SplineClosed,
  {ControlPoints, SplineWeights}, SplineKnots, ?, WorkingPrecision, "Unevaluated"]

I don't know what the second argument means (it seems to always be a list with rank repeats of {0., 1.}), and the last argument seems to always be "Unevaluated". It looks like changing any of them doesn't affect the spline. There is also an argument before WorkingPrecision which I was unable to identify – it corresponds to DerivativeOrder as shown in xzczd's answer.