Do not understand evaluation order of ReplaceAll

Question

{x, x^2, Length@x, Subsets[x]} /. x -> {1, 2, 3}   
(* {{1, 2, 3}, {1, 4, 9}, 0, {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}} *)

with error

What does it mean?

Why ^ evaluates, but Length not?

Why there is correct result of Subsets in output, but raised error?

---

UPD:
Many thanks to all for the detailed explanations!
Still the question was interesting

Answer 1

Let me repeat again:

If a function doesn't have a HoldAll/HoldFirst/HoldRest/HoldAllComplete attribute, its argument(s) will always be evaluated before going into the function.

ReplaceAll (/.) doesn't have such attribute, so the whole {x, x^2, Length@x, Subsets[x]} evaluates before the replacement happens. (The order is from left to right, BTW. ) This can be checked with Trace:

Trace[{x, x^2, Length[x], Subsets[x]} /. x -> {1, 2, 3}]

If you want to check the evaluation of x and x^2, set TraceOriginal -> True, the output will be a bit more involved, though.

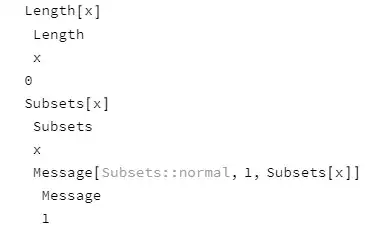
As we can see, Length@x evaluates to 0. This is expected. As mentioned in Details section of document of Length:

Length[expr] returns 0 whenever AtomQ[expr] is True.

Subsets[x] evaluates to itself with a warning Subsets::normal. Since the Subsets[x] is still there, once the replacement happens, it'll become Subsets[{1, 2, 3}] and further evaluates to the desired output.

Finally, in addition to the Hold & ReleaseHold technique shown in rhermans' answer, another (more advanced) way to adjust the evaluation order is to use Unevaluated:

Unevaluated@{x, x^2, Length[x], Subsets[x]} /. x -> {1, 2, 3}
(* {{1, 2, 3}, {1, 4, 9}, 3, {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}} *)

Answer 2

What's happening on your code

You can check the evaluation with TracePrint. You will see that the Left hand side does get evaluated before the replacement. At that first evaluation x^2 returns unchanged, Subsets[x] gives an error and also returns unchanged. Length[x] evaluates and returns 0.

TracePrint[
{x, x^2, Length@x, Subsets[x]} /. x -> {1, 2, 3}   
]

You could have investigated the error with Show Stack Trace.

One of many solutions to what you ask

You could avoid the left hand side been evaluated by using Hold and only ReleaseHold after ReplaceAll (/.) has evaluated. That will avoid the error from trying to evaluate Subsets[x] and have Length return the length of {1, 2, 3} (3) instead of the length of x (0).

ReleaseHold[
     Hold[{x, x^2, Length@x, Subsets[x]}] /. x -> {1, 2, 3}   
]

This does evaluate in the order you want

Answers

This is a rather abstract and advanced issue, it's ok to find it complicated. I struggled articulating a precise answer myself.

What does it mean?

It means you need to consider in which order thigs are evaluated, and how many times that happens. You can control that order in many ways. See Evaluation Control.

Why ^ evaluates, but Length not?

Both evaluate. Length[x] evaluates to 0. Power[x,2] evaluates but first returns unchanged, and remains unchanged until ReplaceAll evaluates changing x for {1,2,3}. Then Power[{1,2,3},2] evaluates to {1,4,9}.

Why there is correct result of Subsets in output, but raised error?

Because it first tries to evaluate Subsets[x], gives an error and returns unchanged. Then ReplaceAll evaluates, and now Subsets[{1, 2, 3}] can evaluate correctly and give an output different from the input.