I am having trouble scaling a set of coordinates and generating these coordinates into stepwise functions.
I start with the points from a plot:
points = {{395.4416644777464`,
207.63931734339303`}, {391.15890276860114`,
240.47382378017346`}, {382.59337935031067`,
219.06001523444706`}, {378.3106176411653`,
209.0669045797748`}, {369.74509422287485`,
177.65998537937617`}, {361.1795708045843`,
250.4669344348457`}, {355.46922185905726`,
204.78414287062958`}, {346.9036984407667`,
236.19106207102823`}, {341.19334949523966`,
184.79792156128497`}, {332.6278260769492`,
220.48760247082885`}, {326.9174771314222`,
214.77725352530183`}, {322.6347154222768`,
260.4600450895181`}, {316.9243664767498`,
219.06001523444706`}, {314.06919200398636`,
241.90141101655524`}, {304.076081349314`,
119.12890868772422`}, {295.5105579310235`,
327.5566451994606`}, {278.3795110944425`,
156.24617683364988`}, {269.8139876761519`,
251.8945216712275`}, {264.1036387306249`,
196.218619452339`}, {258.39328978509786`,
286.1566153443896`}, {249.8277663668073`,
233.33588759826466`}, {241.26224294851679`,
173.37722367023093`}, {231.26913229384448`,
184.79792156128497`}, {224.13119611193568`,
286.1566153443896`}, {215.56567269364515`,
160.52893854279512`}, {199.86221309344583`,
303.28766218097076`}, {184.1587534932465`,
72.01852988712619`}, {172.73805560219247`,
587.3775222209401`}, {162.74494494752017`,
83.43922777818022`}, {149.89665982008435`,
260.4600450895181`}, {145.61389811093912`,
254.74969614399106`}, {138.47596192903032`,
317.56353454478824`}, {131.33802574712158`,
183.37033432490318`}, {124.20008956521278`,
193.36344497957543`}, {119.91732785606749`,
160.52893854279512`}, {112.77939167415872`,
214.77725352530183`}, {108.49662996501345`,
199.07379392510256`}, {105.64145549224995`,
250.4669344348457`}, {101.35869378310466`,
324.70147072669704`}, {98.50351931034115`,
224.77036417997408`}, {91.36558312843238`,
220.48760247082885`}, {81.37247247376007`,
96.28751290561604`}, {75.66212352823305`,
200.50138116148423`}, {72.80694905546954`,
351.82562821795045`}, {54.24831498250671`,
154.8185895972681`}, {41.4000298550709`,
240.47382378017346`}, {35.68968090954388`,
236.19106207102823`}, {32.83450643678037`,
280.4462663988626`}, {12.848285127435787`,
131.97719381515992`}, {7.1379361819087705`, 227.62553865273765`}};
Then I generate a time-dependent stepwise function:
Clear[t];
f[t_] = Piecewise[
Partition[Sort[points], 2,
1] /. {{a_?NumericQ, b_}, {c_, d_}} :> {b, a <= t < c}];
which I then shift to put the highest peak to the y-axis:
f1[t_] = f[(172.73805560219247` (t + Pi)/Pi)];
Plot[f1[t], {t, -Pi, Pi}]
This gives a nice plot:
which of the function I can transform to a Fourier series:
FD[t_] = FourierSeries[f1[t], t, 15]
and plot to a nice function:
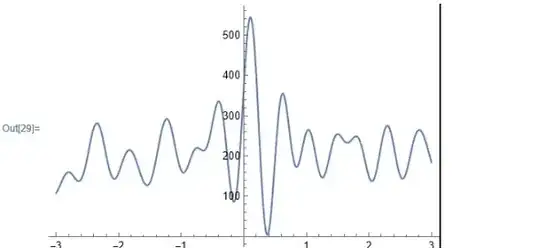
Plot[{FD[t]}, {t, -3, 3}, PlotRange -> Full]
Once done this, which is all fine, I then go over to generating the same piecewise function as above, but not time-dependent, but position dependent. In order to do this, I simply scale the coordinates by the command:
pointsq = ScalingTransform[{15, 1}][points]
again, generate a piecewise function:
f[x_] = Piecewise[
Partition[Sort[pointsq], 2,
1] /. {{a_?NumericQ, b_}, {c_, d_}} :> {b, a <= x < c}];
Shift the coordinates so the highest peak is at the origin:
f1[x_] = f[(2591.070834032887` (x + Pi)/Pi)];
Plot[f1[x], {x, -Pi, Pi}]
then I obtain a Fourier-series by:
ud[x_] = FourierSeries[f1[x], x, 15]
The interesting thing is that even these functions should be different, they look the same:
Here is the Fourier series of the time-independent (position dependent ) function:
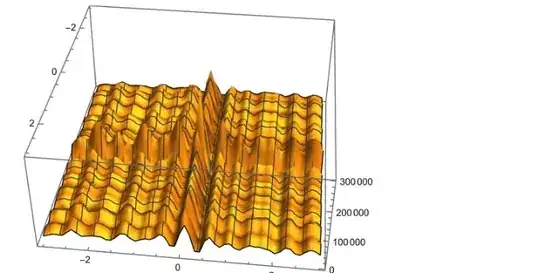
and when I plot these two as $f(t)\cdot u(x)$ I get a symmetric plot, which means the are equal:
So the Fourier transform gives the same result, because the function is only scaled by a scalar. So if this is caused by the Fourier transform it self, or not, I don't know.
So, how can I "stretch" the x-axis on the given plot of the Fourier series by the scaled factor I used for the point-set (the factor is 2591.070834032887`)? The function to stretch is $ud(x)$
Thanks


FourierSeriesrather thanFourier? There is also the optionFourierParameters. Do my notes onFourierhelp? – Hugh Feb 28 '23 at 11:34