0

I have a list of data in the form of {x,y} (30K only). The discrete data give two curves with a cross point.

pts = ToExpression /@ Import["~\\testdata.csv"];
ListPlot[pts, PlotRange -> {{0, 3}, {-1, 0.1}}, Frame -> True, ImageSize -> 300, AspectRatio -> 0.6]

enter image description here

My goal:

I would like to plot 2 independent smooth curves according to these points in one graphic as follows. The 2 curves are expected based on their physical meaning.

enter image description here

My trial:

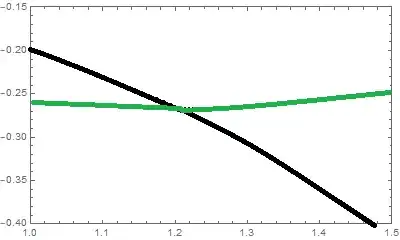
  1. I have tried to separate the two curves using the Unshuffle function provided by @Victor K. in this answer, but it seems that when the two curves are crossing, that code cannot separate them as expected.

    {LstA, LstB} = Unshuffle[pts]; unshufflePlot = ListPlot[{LstA, LstB}, PlotStyle -> {Black, Green}, PlotRange -> {{1, 1.5}, {-0.4, -0.15}}, Frame -> True, ImageSize -> 400, AspectRatio -> 0.6]

enter image description here

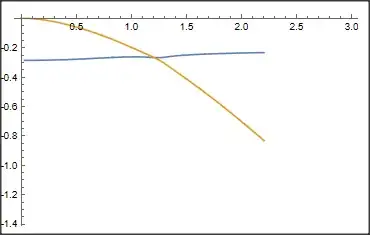
  1. I also tried FindCurvePath, which even only gives a small part of the plot...

    curves = FindCurvePath[pts]; FindCurvePlot = ListLinePlot[pts[[curves[1]]], PlotRange -> {{1, 1.5}, {-0.4, -0.15}}, Frame -> True, ImageSize -> 400, AspectRatio -> 0.6]

enter image description here

  1. As suggested by @Domen, I tried the findCurves function in this link, however, it still cannot separate the different curves from the mixed dataset. What it gives is some mixed curves depending on the value of eps in findCurves.

Now, I have no idea to solve this problem. Can someone give some suggestions? Thank you in advance :)

lxy
  • 165
  • 5
  • 19
  • Your question is very similar to this Q&A have you tried the approach on those answers? – rhermans Mar 01 '23 at 12:30
  • @Jsxs Your question has been flagged as a duplicate. Please [edit] your question to explain how is it different from the other similar questions on the site. Otherwise you risk having the question closed, unable to receive further answers. – rhermans Mar 01 '23 at 14:10
  • @rhermans, thank you for your suggestion. I have tested with the answer in the post you provided, that method gives two curves as a whole. Please also see my update. – lxy Mar 01 '23 at 14:32
  • "it still cannot separate the different curves from the mixed dataset" is not enough, you have to show your diligence. Please explain what fails and how, show your code attempts, show the outputs. You are making it hard to help you. – rhermans Mar 01 '23 at 14:34
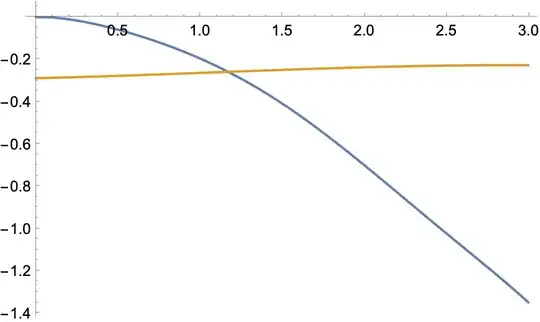
  • @jsxs, using my answer from question provided above as curves = findCurves[data, .03] produces desired results. – Domen Mar 01 '23 at 14:38

2 Answers2

1

Your data has a simple structure with some flaws. The main feature is that there is always one point of one curve and then a point of the other curve. Therefore, I think one should exploit this feature.

However, there are some irregularities tat need fixing. The first 6 point belong exclusively to curve 2. Then there are 3 points without a partner on the other curve, namely point no.: 351,380,381. Further from point no.: 878 the curves are reversed.

To fix this, we may first reverse the order of the points from point no:. 878 on:

pts[[878 ;;]] = Transpose[Reverse /@ Partition[pts[[878 ;;]], 2]];

Then we can delete the singular points:

pts = Delete[pts, {{351}, {980}, {981}}];

Finally we may disassemble the points by taking the first 6 points:

d0 = dat[[;; 6]];

Then we partition the rest of the points according to the 2 curves:

{d1, d2} = Transpose[Partition[pts[[7 ;;]], 2]];

Then we add the first 6 points to curve 2:

d2 = Join[d0, d2];

Now we have the points separated into 2 curves:

ListLinePlot[{d1, d2}]

enter image description here

If you want functions, you can write:

f1= Interpolation[d1];
f2= Interpolation[d2];
Daniel Huber
  • 51,463
  • 1
  • 23
  • 57
1
Clear["Global`*"]

pts = Import["/Users/roberthanlon/Downloads/testdata.csv", "Data"];

{xmin, xmax} = MinMax[pts[[All, 1]]]

(* {0., 2.995} *)

Use FindCurvePath to separate the segments

pts4 = pts[[#]] & /@ FindCurvePath[pts];

ListLinePlot[pts4,
 PlotRange -> All,
 PlotLegends -> Placed[Automatic, {.3, .4}]]

enter image description here

Join the line segments

pts2 = {Join[pts4[[1]], pts4[[3]]], Join[pts4[[2]], pts4[[4]]]};

Using FindFormula to fit the curves

funcs = FindFormula[#, x] & /@ pts2

(* {0.0176757 x - 0.419725 x^2 + 0.416205 x^3 - 0.292456 x^4 + 
     0.0928377 x^5 - 0.0106112 x^6, 
   -0.288809 + 0.0187772 x + 0.00952705 x^2 - 0.00298774 x^3} *)


Plot[funcs, {x, xmin, xmax}]

enter image description here

Bob Hanlon
  • 157,611
  • 7
  • 77
  • 198