FEM code working well in v.12.1, has warning in v.13, and not working in v.13.2.1

Question

Let us consider sound in a glass. Numerical model has been described here. FEM code is given by

<< NDSolve`FEM`;
L = 0.14; L1 = 0.01; del = 0.003; r1 = 0.085/2; r2 = 0.055/2;
polygon = 
  Polygon[{{0, 0, 0}, {r2 + del, 0, 0}, {r2 + del, 0, L1}, {r1 + del, 
     0, L}, {r1, 0, L}, {r2, 0, L1}, {0, 0, L1}}];
Needs["OpenCascadeLink`"]
shape = OpenCascadeShape[polygon];
axis = {{0, 0, 0}, {0, 0, 3/2 L}}; sweep = 
 OpenCascadeShapeRotationalSweep[shape, axis, 2 Pi];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep, 
   "ShapeSurfaceMeshOptions" -> {"LinearDeflection" -> 0.0003}];
Show[Graphics3D[{{Red, polygon}, {Blue, Thick, Arrow[axis]}}], 
 bmesh["Wireframe"], Boxed -> False]
mesh = ToElementMesh[bmesh, AccuracyGoal -> 5, PrecisionGoal -> 5, 
  "MeshOrder" -> 1]
mesh["Wireframe"]
param = {Y -> 5610^9, [Nu] -> 25/100}; rho = 2500; cg = 
 Sqrt[56.10^9/rho]; nu = 1;
ClearAll[stressOperator];
stressOperator[
   Y_, [Nu]_] := {Inactive[
      Div][{{0, 0, -((Y*[Nu])/((1 - 2[Nu])(1 + [Nu])))}, {0, 0, 
        0}, {-Y/(2(1 + [Nu])), 0, 0}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, -((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 
        0}, {-Y/(2(1 + [Nu])), 0, 0}, {0, 0, 0}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu]))), 0, 
        0}, {0, -Y/(2(1 + [Nu])), 0}, {0, 0, -Y/(2(1 + [Nu]))}} . 
      Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}], 
   Inactive[
      Div][{{0, 0, 0}, {0, 
        0, -((Y*[Nu])/((1 - 
               2[Nu])(1 + [Nu])))}, {0, -Y/(2(1 + [Nu])), 0}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, -Y/(2(1 + [Nu])), 
        0}, {-((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 0, 0}, {0, 0, 
        0}} . Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-Y/(2(1 + [Nu])), 0, 
        0}, {0, -((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu]))), 
        0}, {0, 0, -Y/(2(1 + [Nu]))}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}], 
   Inactive[
      Div][{{0, 0, 0}, {0, 
        0, -Y/(2*(1 + [Nu]))}, {0, -((Y[Nu])/((1 - 
               2[Nu])(1 + [Nu]))), 0}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, 0, -Y/(2(1 + [Nu]))}, {0, 0, 
        0}, {-((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 0, 0}} . 
      Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-Y/(2(1 + [Nu])), 0, 0}, {0, -Y/(2(1 + [Nu])), 
        0}, {0, 0, -((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu])))}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}]};
{vals, funs} = 
 NDEigensystem[{stressOperator[56*10^9, 1/4] + 
     rho {D[u[t, x, y, z], {t, 2}], D[v[t, x, y, z], {t, 2}], 
       D[w[t, x, y, z], {t, 2}]} + 
     0 nu {D[u[t, x, y, z], {t, 1}], D[v[t, x, y, z], {t, 1}], 
       D[w[t, x, y, z], {t, 1}]} == {0, 0, 0}, 
   DirichletCondition[{u[t, x, y, z] == 0, v[t, x, y, z] == 0, 
     w[t, x, y, z] == 0}, z == 0]}, {u, v, w}, 
  t, {x, y, z} [Element] mesh, 12];

In v.12.1 we have

Abs[vals]/(2 Pi)
Out[]= {1973.97, 1973.97, 1974.85, 1974.85, 2169.46, 2169.46, 

2250.23, 2250.23, 4183.75, 4183.75, 5532.1, 5532.1}

In v.13.01 there are two warnings

Eigensystem::maxit2: Warning: maximum number of iterations, 1000, has been reached by the Arnoldi algorithm without convergence to the specified tolerance, but the current best computed value has been returned. You can use method options with Method -> {Arnoldi, opts} to increase the size of basis vectors, the maximum number of iterations, reduce the tolerance, or use an estimate as a shift, any of which may help.
Eigensystem::chnpdef: Warning: there is a possibility that the second matrix SparseArray[Specified elements: 705552
Dimensions: {64620,64620}
in the first argument is not positive definite, which is necessary for the Arnoldi method to give accurate results.

But nevertheless we have same results as above

Abs[vals]/(2 Pi)
Out[]= {1973.97, 1973.97, 1974.85, 1974.85, 2169.46, 2169.46, 

2250.23, 2250.23, 4183.75, 4183.75, 5532.1, 5532.1}

In v.13.2.1 we have 3 warnings and nothing out

Eigensystem::arerr: Could not continue Arnoldi algorithm because the required eigenvectors cannot be computed.
Set::shape: Lists {vals,funs} and NDEigensystem[...,12] are not the same shape.
Eigensystem::arerr: Could not continue Arnoldi algorithm because the required eigenvectors cannot be computed.

What happened with Arnoldi algorithm between v. 12.1 and v.13.2.1?

Update 1. We can force Arnoldi algorithm with using options for NDEigensystem and removing options in mesh generator as follows

<< NDSolve`FEM`;
L = 0.14; L1 = 0.01; del = 0.003; r1 = 0.085/2; r2 = 0.055/2;
polygon = 
  Polygon[{{0, 0, 0}, {r2 + del, 0, 0}, {r2 + del, 0, L1}, {r1 + del, 
     0, L}, {r1, 0, L}, {r2, 0, L1}, {0, 0, L1}}];
Needs["OpenCascadeLink`"]
shape = OpenCascadeShape[polygon];
axis = {{0, 0, 0}, {0, 0, 3/2 L}}; sweep = 
 OpenCascadeShapeRotationalSweep[shape, axis, 2 Pi];
bmesh = OpenCascadeShapeSurfaceMeshToBoundaryMesh[sweep, 
   "ShapeSurfaceMeshOptions" -> {"LinearDeflection" -> 0.0003}];
Show[Graphics3D[{{Red, polygon}, {Blue, Thick, Arrow[axis]}}], 
 bmesh["Wireframe"], Boxed -> False] 
mesh = ToElementMesh[bmesh]
mesh["Wireframe"]
param = {Y -> 5610^9, [Nu] -> 25/100}; rho = 2500; cg = 
 Sqrt[56.10^9/rho]; nu = 1;
ClearAll[stressOperator];
stressOperator[
   Y_, [Nu]_] := {Inactive[
      Div][{{0, 0, -((Y*[Nu])/((1 - 2[Nu])(1 + [Nu])))}, {0, 0, 
        0}, {-Y/(2(1 + [Nu])), 0, 0}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, -((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 
        0}, {-Y/(2(1 + [Nu])), 0, 0}, {0, 0, 0}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu]))), 0, 
        0}, {0, -Y/(2(1 + [Nu])), 0}, {0, 0, -Y/(2(1 + [Nu]))}} . 
      Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}], 
   Inactive[
      Div][{{0, 0, 0}, {0, 
        0, -((Y*[Nu])/((1 - 
               2[Nu])(1 + [Nu])))}, {0, -Y/(2(1 + [Nu])), 0}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, -Y/(2(1 + [Nu])), 
        0}, {-((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 0, 0}, {0, 0, 
        0}} . Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-Y/(2(1 + [Nu])), 0, 
        0}, {0, -((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu]))), 
        0}, {0, 0, -Y/(2(1 + [Nu]))}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}], 
   Inactive[
      Div][{{0, 0, 0}, {0, 
        0, -Y/(2*(1 + [Nu]))}, {0, -((Y[Nu])/((1 - 
               2[Nu])(1 + [Nu]))), 0}} . 
      Inactive[Grad][v[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{0, 0, -Y/(2(1 + [Nu]))}, {0, 0, 
        0}, {-((Y[Nu])/((1 - 2[Nu])(1 + [Nu]))), 0, 0}} . 
      Inactive[Grad][u[t, x, y, z], {x, y, z}], {x, y, z}] + 
    Inactive[
      Div][{{-Y/(2(1 + [Nu])), 0, 0}, {0, -Y/(2(1 + [Nu])), 
        0}, {0, 0, -((Y(1 - [Nu]))/((1 - 2[Nu])(1 + [Nu])))}} . 
      Inactive[Grad][w[t, x, y, z], {x, y, z}], {x, y, z}]};
{vals, funs} = 
 NDEigensystem[{stressOperator[56.*10^9, 1./4] + 
     rho {D[u[t, x, y, z], {t, 2}], D[v[t, x, y, z], {t, 2}], 
       D[w[t, x, y, z], {t, 2}]} + 
     0 nu {D[u[t, x, y, z], {t, 1}], D[v[t, x, y, z], {t, 1}], 
       D[w[t, x, y, z], {t, 1}]} == {0, 0, 0}, 
   DirichletCondition[{u[t, x, y, z] == 0, v[t, x, y, z] == 0, 
     w[t, x, y, z] == 0}, z == 0]}, {u, v, w}, 
  t, {x, y, z} [Element] mesh, 6, 
  Method -> {"Eigensystem" -> {"Arnoldi", "MaxIterations" -> 1000, 
      Tolerance -> 0.01}}];

With this code we have

Abs[vals]/(2 Pi)
Out[]= {1375.35, 1375.35, 1375.4, 1375.4, 1943.75, 1943.75}

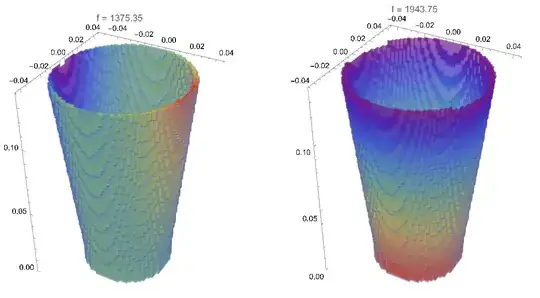
This result is differ from that we discussed here. Nevertheless visualization shows that fifth eigenfunction looks like fifth one in v.12.1,

{DensityPlot3D[Re[funs[[1, 1]][x, y, z]], {x, y, z} \[Element] mesh, 
 ColorFunction -> "Rainbow", OpacityFunction -> None, Boxed -> False, 
 PlotLabel -> Row[{"f = ", Abs[vals [[1]]]/2/Pi}], 
 BoxRatios -> Automatic, PlotPoints -> 50], DensityPlot3D[Re[funs[[5, 1]][x, y, z]], {x, y, z} \[Element] mesh, 
 ColorFunction -> "Rainbow", OpacityFunction -> None, Boxed -> False, 
 PlotLabel -> Row[{"f = ", Abs[vals [[5]]]/2/Pi}], 
 BoxRatios -> Automatic, PlotPoints -> 50]}

Update 2. As it mentioned by user21 we generate mesh in v.12.2 and then export it in v.13.2 using DumpSave["mesh.mx", mesh] in v.12.2 and << mesh.mx in v.13.2. The result of

{vals, funs} = 
  NDEigensystem[{stressOperator[56*10^9, 1/4] + 
      rho {D[u[t, x, y, z], {t, 2}], D[v[t, x, y, z], {t, 2}], 
        D[w[t, x, y, z], {t, 2}]} + 
      0 nu {D[u[t, x, y, z], {t, 1}], D[v[t, x, y, z], {t, 1}], 
        D[w[t, x, y, z], {t, 1}]} == {0, 0, 0}, 
    DirichletCondition[{u[t, x, y, z] == 0, v[t, x, y, z] == 0, 
      w[t, x, y, z] == 0}, z == 0]}, {u, v, w}, 
   t, {x, y, z} \[Element] mesh, 12];

in v.13.2 is same as in v.12.2. For example,

Abs[vals]/(2 Pi)
Out[]= {1973.97, 1973.97, 1974.85, 1974.85, 2169.46, 2169.46, 

2250.23, 2250.23, 4183.75, 4183.75, 5532.1, 5532.1}

Visualization

{DensityPlot3D[Re[funs[[1, 1]][x, y, z]], {x, y, z} \[Element] mesh, 
 ColorFunction -> "Rainbow", OpacityFunction -> None, Boxed -> False, 
 PlotLabel -> Row[{"f = ", Abs[vals [[1]]]/2/Pi}], 
 BoxRatios -> Automatic, PlotPoints -> 50],DensityPlot3D[
  Re[funs[[5, 1]][x, y, z]], {x, y, z} \[Element] mesh, 
  ColorFunction -> "Rainbow", OpacityFunction -> None, Boxed -> False,
   PlotLabel -> Row[{"f = ", Abs[vals[[5]]]/2/Pi}], 
  BoxRatios -> Automatic, PlotPoints -> 50],
 DensityPlot3D[Re[funs[[7, 1]][x, y, z]], {x, y, z} \[Element] mesh, 
  ColorFunction -> "Rainbow", OpacityFunction -> None, Boxed -> False,
   PlotLabel -> Row[{"f = ", Abs[vals[[7]]]/2/Pi}], 
  BoxRatios -> Automatic, PlotPoints -> 50]}

@user21 This is $Version out "13.2.1 for Microsoft Windows (64-bit) (January 27, 2023)" — Alex Trounev, Mar 10 '23 at 13:59
Hm. Unfortunately, I do not have 12.1 installed. Could you try and export the mesh from 12.1 and then import the mesh into 13.2 and see if the message is still there? — user21, Mar 13 '23 at 13:57
@user21 I got some options to force the Arnoldi algorithm in v.13.2.1 - see Update 1. — Alex Trounev, Mar 13 '23 at 17:15
"in the first argument is not positive definite, which is necessary for the Arnoldi method to give accurate results." if that is true Mathematica is right to block further execution. No? — Валерий Заподовников, Mar 14 '23 at 04:32
The message chnpdef has been generated after 1000 iterations. So it indicates current state on thousandth iteration. Usually in this case Mathematica gives some solution defined as the best one. — Alex Trounev, Mar 14 '23 at 04:56
Why not use normal solvers like FEAST or FGMRES? Arnoldi is ancient. — Валерий Заподовников, Mar 14 '23 at 09:36
I remember that in previous version this was very sensitive to the mesh. Did you get a chance and try to import the mesh from 12.1 and see if the old mesh produces the same result. Then we'd know that this is a mesh issue and not a solver issue. — user21, Mar 21 '23 at 05:59
@user21 Not yet, since some solution has been evaluated with mesh generated in v.13.2 as well. This solution is different from v12.1 and 13.01. But it is better than nothing. — Alex Trounev, Mar 21 '23 at 08:52

user21 · Accepted Answer · 2023-04-14T07:32:04.660

1

I have been prompted of off this channel to comment on this issue. So this is a comment and not an answer.

The issue here is not so much that the behavior changed between version. If one goes through the original post one can see that even in that original post there were issues with mesh dependence of the solution; mesh dependence in the sense of the solution is sensitive to the mesh used. In other words even in version 12.1 there were problems. What should be done, is to export the mesh from version 12.1 and import it into 13.2.1 on exactly the same hardware and see if the problem persists. If the problem goes away, then we know that the issue in 13.2.1 is caused by the mesh. I suspect it will go away. Then the more relevant question, I feel, is why is the original problem so mesh dependent. To that I do not know the answer.

edited Apr 14 '23 at 07:32

answered Apr 14 '23 at 06:42

user21

39,710
8
110
167

Thank you very much for your answer. Did you read Update 1 to my post? – Alex Trounev Apr 14 '23 at 07:21
@AlexTrounev, yes, I did see that. I am wondering if we use the mesh from 12.1 and run the original code in 13.2.1 just with the mesh from (12.1) if that gives the same result as 12.1 did. I suspect it will. – user21 Apr 14 '23 at 07:33
You are right. I did SetDirectory[$TemporaryDirectory] and DumpSave["mesh.mx", mesh] in v.12.2, then in v.13.2 I did SetDirectory[$TemporaryDirectory] and << mesh.mx. Finally I used mesh generated in v12.2 to compute NDEigensystem in v.13.2. Results are same as in v. 12.2. Therefore, we have some mesh issues in v.13.2. – Alex Trounev Apr 14 '23 at 09:42
@AlexTrounev, I do not think there is a mesh issue in 13.2. the real issue is that the model per se is sensitive to changes in the mesh. Also in version 12.2 it is possible to create meshes that do not converge. – user21 Apr 17 '23 at 04:53

FEM code working well in v.12.1, has warning in v.13, and not working in v.13.2.1

1 Answers1