1

I want to solve a simple diffuse equation in a cylinder.

$\nabla\cdot(\hat{c}\nabla\rho_P）=0$

$\rho_P(x,y,\theta)==0,\sqrt{x^2+y^2}=R$

$\rho_P(0,0,\theta)==1,\sqrt{x^2+y^2}=0$

$\rho_P(x,y,2\pi)=\rho_P(x,y,0)$

$\hat{c}=\begin{pmatrix} D_t& 0& 0 \\ 0 & D_t &0\\0 &0 &D_r \end{pmatrix} \quad$

$D_t: transportation\ coefficient$

$D_r: rotation\ coefficient$

Needs["NDSolve`FEM`"]

{R, Difft, Diffr} = {29.5, 1, 0.01};
[CapitalOmega] = Cylinder[{{0, 0, 0}, {0, 0, 2 [Pi]}}, R];


c = {{Difft, 0, 0}, {0, Difft, 0}, {0, 0, Diffr}};


With[{rhop = rhop[x, y, [Theta]]}, 
  op1 = Div[c . Grad[rhop, {x, y, [Theta]}], {x, y, [Theta]}]];


Subscript[[CapitalGamma], D1] = 
  DirichletCondition[rhop[x, y, [Theta]] == 1, 
   x^2 + y^2 == 0 && [Theta] != 2 [Pi]];
Subscript[[CapitalGamma], D2] = 
  DirichletCondition[rhop[x, y, [Theta]] == 0, 
   x^2 + y^2 > 0 && [Theta] != 0 && [Theta] != 2 [Pi]];
Subscript[[CapitalGamma], p] = 
  PeriodicBoundaryCondition[rhop[x, y, [Theta]], [Theta] == 2 [Pi],
    Function[[Theta], [Theta] - 2 [Pi]]];


cylinderMesh = 
  ToElementMesh[[CapitalOmega], "MaxBoundaryCellMeasure" -> 0.04];


npfun = NDSolveValue[{op1 == 0, Subscript[[CapitalGamma], p], 
    Subscript[[CapitalGamma], D1], Subscript[[CapitalGamma], D2]}, 
   rhop, {x, y, [Theta]} [Element] cylinderMesh];


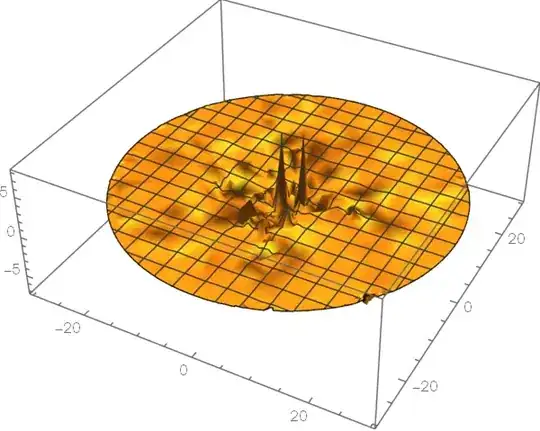
ContourPlot[npfun[x, y, 2 [Pi]], {x, y} [Element] Disk[{0, 0}, R], 
 PlotRange -> All]

Obviously, it is a symmetrical function, but when I solve it using NDSolveValue, the result is not symmetric. enter image description here

I think I can solve it by adding

additionalPoints = {{0, 0, 0}, {0, 0, 2 \[Pi]}}
cylinderMesh = 
  ToElementMesh[\[CapitalOmega], "IncludePoints" -> additionalPoints];

But the error: enter image description here 无法产生网络：enable to generate mesh

江蛮子
  • 85
  • 5
  • Your second DirichletCondition should be Subscript[\[CapitalGamma], D2] = DirichletCondition[rhop[x, y, \[Theta]] == 0, x^2 + y^2 ==R^2 && \[Theta] != 0 && \[Theta] != 2 \[Pi]] – Ulrich Neumann Mar 16 '23 at 09:38
  • Region Cylinder suggest a 3D problem, but I'm missing an axial z coordinate!? – Ulrich Neumann Mar 16 '23 at 11:05
  • but,if i write as Subscript[\[CapitalGamma], D1] = DirichletCondition[rhop[x, y, \[Theta]] == 1, x^2 + y^2 == 0 && \[Theta] != 0 && \[Theta] != 2 \[Pi]];, Subscript[\[CapitalGamma], D2] = DirichletCondition[rhop[x, y, \[Theta]] == 0, x^2 + y^2 == R^2 && \[Theta] != 0 && \[Theta] != 2 \[Pi]]; there is a error: NDSolveValue::bcnop: No position was found on the boundary where x^2+y^2==0&&\[Theta]!=0&\[Theta]!=2 \[Pi] is true, so DirichletCondition[rhop==1,x^2+y^2==0&&\[Theta]!=0&&[Theta]!=2 \[Pi]]. will be ignored – 江蛮子 Mar 17 '23 at 00:58
  • I think I should add a line(0,0,theta) or points(0,0,2pi)(0,0,0) to the mesh, but i can't find the option. – 江蛮子 Mar 17 '23 at 01:04
  • Is \[Theta the axial coordinate(not an angle of polarcoordinates)? – Ulrich Neumann Mar 17 '23 at 08:27
  • yes, z is theta – 江蛮子 Mar 17 '23 at 10:56
  • 1
    The problem is not well-posed. Subscript[\[CapitalGamma], D2] already determines the solution, you cannot force b.c. at x^2+y^2==0, because it's the removable singularity in cylindrical coordinates. Related: https://mathematica.stackexchange.com/questions/245195/laplaces-equation-in-spherical-coordinates-with-neumann-b-c/245309#comment617526_245309 – xzczd Mar 17 '23 at 12:44

1 Answers1

2

I modified your code a little bit. You need two periodic boundaryconditions with correct TranslationTransform in all coordinates. Additionally I force NDSolve to use FiniteElement- Method (no need to load Needs["NDSolveFEM"])

I changed the Region \[CapitalOmega] to avoid singularity x^2+y^2->0. Play around with the new small parameter dR.

It is often recommended to rationalize the parameters.

{R, dR, Difft, Diffr} = {29.5, 29.5/100, 1, 0.01}// Rationalize[#, 0]&;
\[CapitalOmega] =RegionDifference[Cylinder[{{0, 0, 0}, {0, 0, 2 \[Pi] }},R], Cylinder[{{0, 0, 0}, {0, 0, 2 \[Pi] }}, dR]];

Try

c = {{Difft, 0, 0}, {0, Difft, 0}, {0, 0, Diffr}};

With[{rhop = rhop[x, y, [Theta]]},op1 = Div[c . Grad[rhop, {x, y, [Theta]}], {x, y, [Theta]}]];


[CapitalGamma]D1 =DirichletCondition[rhop[x, y, [Theta]] == 1,x^2 + y^2 == dR^2 && 0 < [Theta] < 2 [Pi]];
[CapitalGamma]D2 =DirichletCondition[rhop[x, y, [Theta]] == 0,x^2 + y^2 == R^2 && 0 < [Theta] < 2 [Pi]];
[CapitalGamma]p = {PeriodicBoundaryCondition[rhop[x, y, [Theta]], [Theta] >= 2 [Pi] &&dR^2 < x^2 + y^2 < R^2, TranslationTransform[{0, 0, -2 Pi}]],PeriodicBoundaryCondition[rhop[x, y, [Theta]], [Theta] <= 0 && dR^2 <x^2 + y^2 < R^2, TranslationTransform[{0, 0, +2 Pi}]]};


npfun = NDSolveValue[{op1 ==0, [CapitalGamma]p, [CapitalGamma]D1, [CapitalGamma]D2}, rhop, {x, y, [Theta]} [Element] [CapitalOmega], 
Method -> {"FiniteElement"}]


reg = ImplicitRegion[dR^2 <= x^2 + y^2 <= R^2 , {x, y}]
Plot3D[ npfun[x, y,  [Pi]]  , {x, y} [Element] reg,PlotRange -> All , Mesh -> False]

enter image description here

NDSolve now evaluates a solution which is plausible.

The periodic boundary conditions are fullfiled quite well:

Plot3D[Evaluate[npfun[x, y, 2 \[Pi]] - npfun[x, y, 0]], {x, y}\[Element] reg,PlotRange -> All]

enter image description here

Plot3D[Evaluate[Derivative[0, 0, 1][npfun][x, y, 2 \[Pi]] -Derivative[0, 0, 1][npfun][x, y, 0]], {x, y} \[Element] reg, PlotRange-> All]

enter image description here

I think you might get much better results if you formulate the underlying problem in "Cylindrical"-coordinates!

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55