Poorly behaved ContourPlot

Question

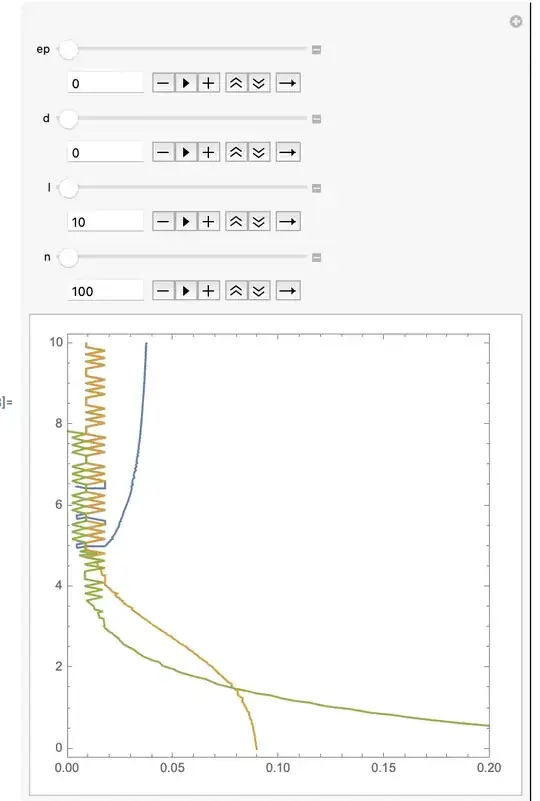
I am interested in finding the interested in finding the intersections of the curves f1==0,f2==0 and g==0 (defined below). My initial idea (which has served me well in the past) was to an implementation of Wagon's FindAllCrossings2D[] (discussed here).

However, before I embarked on that enterprise, I decided to play around with ContourPlot to see what my functions look like. I have included a code snippet below. My primary issue is the visualizations produced by ContourPlot aren't particularly well behaved. I have included some screenshots to demonstrate this.

First for d=0 case shown below, the contours look somewhat reasonably except for the the jagged lines for small c. I have played around with MaxRecursion and setting Exclusions -> True to remedy this but to no avail.

Is there someway to fix this behavior for ContourPlot? Alternatively, is there some other method to a) find the zero level contours for these functions and (b) determine their intersection points?

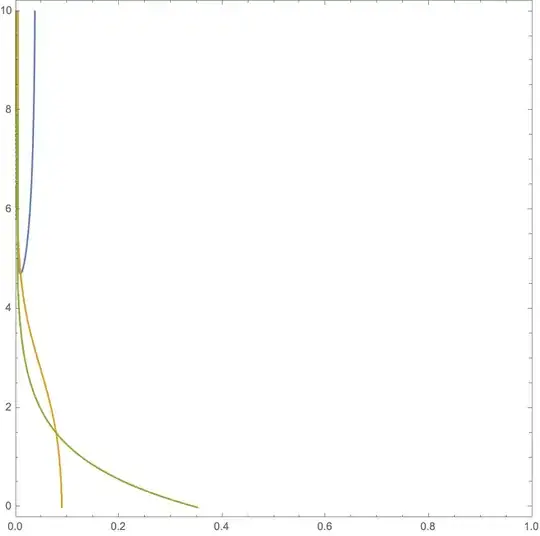
Update Resolved thanks to user @demm incrasing PlotPoints solves this issue.

lmb[c_, ea_, ep_, d_, l_] := (z - 2)*Exp[ea]*Exp[-c (ep + d^2/2 )]
p[c_, ea_, ep_, d_, l_] := 
 1 - (Sqrt[(4clmb[c, ea, ep, d, l])/l + 1] - 1)/((
  2clmb[c, ea, ep, d, l])/l)
func[c_, ea_, ep_, d_, l_, n_] := 
 c/nLog[c/(En)] + (1 - c)Log[1 - c] - (zc^2ep)/2 - (zc^2*d^2)/
  4 + c/l (p[c, ea, ep, d, l]/2 + Log[1 - p[c, ea, ep, d, l]])
f[c_, ea_, ep_, d_, l_, n_] := 
  Evaluate[D[func[c, ea, ep, d, l, n], c]];
f1[c_, ea_, ep_, d_, l_, n_] := Evaluate[D[f[c, ea, ep, d, l, n], c]];
f2[c_, ea_, ep_, d_, l_, n_] := Evaluate[D[f1[c, ea, ep, d, l, n], c]];
g[c_, ea_, ep_, d_, l_, n_] := 
  Evaluate[D[c/n (1 - p[c, ea, ep, d, l])^(n/l), c]];
Manipulate[
 ContourPlot[{f1[c, ea, ep, d, l, n] == 0, 
   f2[c, ea, ep, d, l, n] == 0, g[c, ea, ep, d, l, n] == 0},
  {c, 0, 1}, {ea, 0, 10},
  PlotRange -> {{0, 1}, Automatic}], {ep, 0, 0}, {d, 0, 2, 2}, {l, 10,
   10, 5}, {n, 100, 100, 10}]
z=6(hard code this value)

@demm Thanks. I have edited the question to remove the typo. The issues with the plot still remain. The typo was due to copy-paste and me changing my mind about notation last minute as i was creating this — jcp, Mar 16 '23 at 22:04

score 3 · Accepted Answer · answered Mar 16 '23 at 22:38

3

Increase the PlotPoints (it takes sometime to compute!):

    ContourPlot[{f1[c, ea, 0, 0, 10, 100] == 0, f2[c, ea, 0, 0, 10, 100] == 0, g[c, ea, 0, 0, 10, 100] == 0}, {c, 0, 1}, {ea, 0, 10}, 
PlotRange -> {{0, 1}, Automatic}, ImageSize -> 500, PlotPoints -> 60]

answered Mar 16 '23 at 22:38

demm

1,533
9
13

Thank you so much. Increasing the PlotPoints -> 60 was a definite improvement for d=0 case and has resolved the jagged edges issue. However, d!=0, I don't get a continuous blue curve (which is what I would expect) and instead have two vertical lines. There could perhaps be a different cause for this issue? – jcp Mar 16 '23 at 22:47
What value of d do you consider? – demm Mar 17 '23 at 00:58
In the example I provided in the original question I was looking at d=2. But on second thought maybe my expectations were incorrect – jcp Mar 17 '23 at 01:43
1

You can see from Plot3D[{f1[c, ea, 0, 2, 10, 100], 0}, {c, 0, 1}, {ea, 0, 10}] that the intersection of f1 with the 0-plane consists of two lines (these are the ones depicted by the contour plot). – demm Mar 17 '23 at 11:44
yes, indeed. thanks for your the PlotPoints fix. I have accepted and upvoted your answer. – jcp Mar 17 '23 at 15:33

Poorly behaved ContourPlot

1 Answers1