For a parametric Van der Pol oscillator as given
x'[t] == y[t], y'[t] == -0.1*y[t]*(1 + f*Cos[1.0*t])*((x[t])^2 - 1) - 0.41*(x[t])^3 + (0.5^2)*x[t]
for f=6.88, the oscillator gives positive Lyapunov as following the method given in https://mathematica.stackexchange.com/a/185466/66794, which shows the LE with respect to the time steps I have chosen. But I want a plot by varying f from 6.8 to 6.9. I can't understand how to create the loop f from the code. Please help.
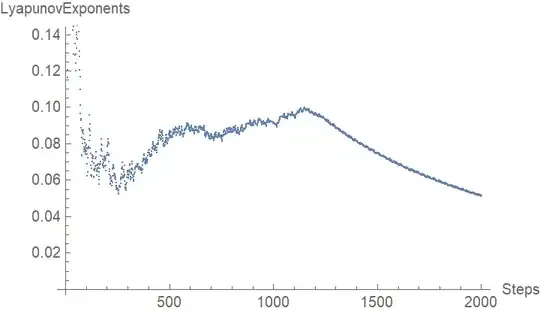
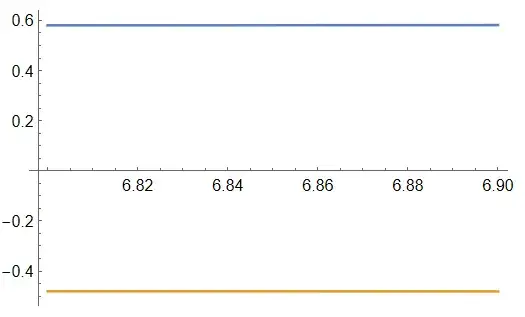

Table:Table[LyapunovExponents[eqns, ics, ShowPlot -> True], {f, 6.8, 6.9, 0.02}]Or do you want all graphs shown in one plot? – Domen Mar 29 '23 at 20:11Lyapunov exponentas a function offinstead ofsteps. @Domen – S Roy Mar 29 '23 at 20:26