How to plot the solutions of nonlinear equations with a parameter varies?

Question

I want to get the solutions of equations with a parameter. But I cannot get a closed-form expressions of x、y. I just want to show how x、y vary with the parameter [Delta]. If i assign values to [Delta],i could get a set of values{x,y}. So how to plot the value of x.y as [Delta] varies? the equations are as follows: [x == 1/3 (2 + y - Sqrt[1 + y + y^2]) && y == -((-2 + Sqrt[ 4 + 3 (-1 + \[Delta])^2 \[Delta] (-2 + (-1 + x)^2 \[Delta])])/( 3 (-1 + \[Delta])^2)) && 0 < y < \[Delta] < x < 1, {x, y}] It's my first time asking question, so may not express clearly in some places. Thanks for your help~

pn =  -((-2 + Sqrt[
   4 + 3 (-1 + \[Delta])^2 \[Delta] (-2 + (-1 + pr)^2 \[Delta])])/(
  3 (-1 + \[Delta])^2));
pr = (2 (1 + pn - s) \[Delta] - 
  Sqrt[\[Delta] (6 + 6 pn - 6 s - 11 \[Delta] + 
     4 (-1 + pn - s) (pn - s) \[Delta] + 6 \[Delta]^2)])/(-3 + 
  6 \[Delta]);
s = 1/12 (8 - (
    4 2^(2/3))/(4 + 54 pn^2 - 27 pn^3 (-1 + \[Delta])^2 + 
      27 pn \[Delta] (-2 + (-1 + pr)^2 \[Delta]) + 
      Sqrt[-16 + (4 + 
         27 pn (2 pn - 
            pn^2 (-1 + \[Delta])^2 + \[Delta] (-2 + (-1 + 
                  pr)^2 \[Delta])))^2])^(1/3) - 
    2 2^(1/3) (4 + 54 pn^2 - 27 pn^3 (-1 + \[Delta])^2 + 
       27 pn \[Delta] (-2 + (-1 + pr)^2 \[Delta]) + 
       Sqrt[-16 + (4 + 
          27 pn (2 pn - 
             pn^2 (-1 + \[Delta])^2 + \[Delta] (-2 + (-1 + 
                   pr)^2 \[Delta])))^2])^(1/3))
limit condition:0 < pn < pr < \[Delta] < 1 && pn > \[Delta] + s - 1 && 0<s<1

So now I want to know if the solution of pr,pn and s exist with the range of parameter [Delta].

The condition 0 < y < \[Delta] < x < 1 is unclear to me. The command Eliminate[ x == 1/3 (2 + y - Sqrt[1 + y + y^2]) && y == -((-2 + Sqrt[4 + 3 (-1 + \[Delta])^2 \[Delta] (-2 + (-1 + x)^2 \[Delta])])/(3 (-1 + \[Delta])^2)), \[Delta]] results in (-1 + 2 x) y == 1 - 4 x + 3 x^2. — user64494, Mar 31 '23 at 09:10
The command Eliminate[ x == 1/3 (2 + y - Sqrt[1 + y + y^2]) && y == -((-2 + Sqrt[4 + 3 (-1 + \[Delta])^2 \[Delta] (-2 + (-1 + x)^2 \[Delta])])/(3 (-1 + \[Delta])^2)), y] results in — user64494, Mar 31 '23 at 09:14
x^3 (84 + 12/(1 - \[Delta]) - 60 \[Delta]) + x (22 + 26/(1 - \[Delta]) - 18 \[Delta]) + x^4 (-31 + 4/(1 - \[Delta]) + 23 \[Delta]) + x^2 (-71 - 39/(1 - \[Delta]) + 53 \[Delta]) == 2 + 5/(1 - \[Delta]) - 2 \[Delta] && x^3 (-96 + 144 \[Delta] - 60 \[Delta]^2) + x (-48 + 40 \[Delta] - 18 \[Delta]^2) + x^4 (27 - 54 \[Delta] + 23 \[Delta]^2) + x^2 (110 - 124 \[Delta] + 53 \[Delta]^2) == -7 + 4 \[Delta] - 2 \[Delta]^2 && -1 + \[Delta] != 0. — user64494, Mar 31 '23 at 09:14
@user64494 0 < y < [Delta] < x < 1 means 0 < y And y< [Delta] And [Delta] < x And x< 1. — , Mar 31 '23 at 17:58

score 0 · Answer 1 · answered Mar 31 '23 at 09:05

Replace the expression for x in y and get the following equation:

eq = y == -((-2 + 
       Sqrt[4 + 3 (-1 + d)^2 d (-2 + (-1 + x)^2 d)])/(3 (-1 + d)^2))

Then solve this equation for y:

ysol[d_] = y /. Solve[eq, y][[1]];

Now there is a divergence near x= 0.72207370945 and a 1/x problem near x=1. Further there can be spurious small imaginary parts from numerical errors. We therefore plot only up to x= 0.9999 and plot only the real part:

Plot[Re[ysol[d]], {d, 0, 0.9999}, PlotRange -> All, 
 Exclusions -> None]

We can restrict the plot range to see more of the behaviour for smaller y:

Plot[Re[ysol[d]], {d, 0, 0.9999}, PlotRange -> {-.1, 0.5}, 
 Exclusions -> None]
Plot[Re[ysol[d]], {d, 0, 0.9999}, PlotRange -> {-200, 0.5}, 
 Exclusions -> None]

As x depends on x it shows the same problems as y:

Plot[Re[1/
    3 (2 + ysol[d] - Sqrt[1 + ysol[d] + ysol[d] ysol[d]^2])], {d, 0, 
  0.9999}, PlotRange -> {0, 0.5}, Exclusions -> None]

score 0 · Answer 2 · answered Mar 31 '23 at 12:09

If I correctly understand the question, this can be done as follows.

Eliminate[  x == 1/3 (2 + y - Sqrt[1 + y + y^2]) &&   
y == -((-2 + Sqrt[4 +  3 (-1 + \[Delta])^2 \[Delta] (-2 + (-1 + x)^2 \[Delta])])/
(3 (-1 + \[Delta])^2)), y]

x^3 (84 + 12/(1 - \[Delta]) - 60 \[Delta]) + x (22 + 26/(1 - \[Delta]) - 18 \[Delta]) + x^4 (-31 + 4/(1 - \[Delta]) + 23 \[Delta]) + x^2 (-71 - 39/(1 - \[Delta]) + 53 \[Delta]) == 2 + 5/(1 - \[Delta]) - 2 \[Delta] && x^3 (-96 + 144 \[Delta] - 60 \[Delta]^2) + x (-48 + 40 \[Delta] - 18 \[Delta]^2) + x^4 (27 - 54 \[Delta] + 23 \[Delta]^2) + x^2 (110 - 124 \[Delta] + 53 \[Delta]^2) == -7 + 4 \[Delta] - 2 \[Delta]^2 && -1 + \[Delta] != 0

The next step consists in

Solve[x^3 (84 + 12/(1 - \[Delta]) - 60 \[Delta]) + 
 x (22 + 26/(1 - \[Delta]) - 18 \[Delta]) + 
 x^4 (-31 + 4/(1 - \[Delta]) + 23 \[Delta]) + 
 x^2 (-71 - 39/(1 - \[Delta]) + 53 \[Delta]) == 
2 + 5/(1 - \[Delta]) - 2 \[Delta] && 
   x^3 (-96 + 144 \[Delta] - 60 \[Delta]^2) + 
 x (-48 + 40 \[Delta] - 18 \[Delta]^2) + 
 x^4 (27 - 54 \[Delta] + 23 \[Delta]^2) + 
 x^2 (110 - 124 \[Delta] + 53 \[Delta]^2) == -7 + 4 \[Delta] - 
 2 \[Delta]^2 && x > \[Delta] && \[Delta] > 0 && \[Delta] < 1&7x<1, x,Reals] // ToRadicals

{{x -> ConditionalExpression[(3 (8 - 12 \[Delta] + 5 \[Delta]^2))/( 27 - 54 \[Delta] + 23 \[Delta]^2) - 1/2 \[Sqrt](( 36 (8 - 12 \[Delta] + 5 \[Delta]^2)^2)/(27 - 54 \[Delta] + 23 \[Delta]^2)^2 - ( 2 (110 - 124 \[Delta] + 53 \[Delta]^2))/( 3 (27 - 54 \[Delta] + 23 \[Delta]^2)) + (2^( 1/3) (544 - 856 \[Delta] + 1104 \[Delta]^2 - 568 \[Delta]^3 + 121 \[Delta]^4))/(3 (27 - 54 \[Delta] + 23 \[Delta]^2) (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^(1/3)) + (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^( 1/3)/(3 2^(1/3) (27 - 54 \[Delta] + 23 \[Delta]^2))) - 1/2 \[Sqrt](( 72 (8 - 12 \[Delta] + 5 \[Delta]^2)^2)/(27 - 54 \[Delta] + 23 \[Delta]^2)^2 - ( 4 (110 - 124 \[Delta] + 53 \[Delta]^2))/( 3 (27 - 54 \[Delta] + 23 \[Delta]^2)) - (2^( 1/3) (544 - 856 \[Delta] + 1104 \[Delta]^2 - 568 \[Delta]^3 + 121 \[Delta]^4))/(3 (27 - 54 \[Delta] + 23 \[Delta]^2) (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^(1/3)) - (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^( 1/3)/(3 2^(1/3) (27 - 54 \[Delta] + 23 \[Delta]^2)) - (( 1728 (8 - 12 \[Delta] + 5 \[Delta]^2)^3)/(27 - 54 \[Delta] + 23 \[Delta]^2)^3 + ( 16 (24 - 20 \[Delta] + 9 \[Delta]^2))/( 27 - 54 \[Delta] + 23 \[Delta]^2) - ( 48 (8 - 12 \[Delta] + 5 \[Delta]^2) (110 - 124 \[Delta] + 53 \[Delta]^2))/(27 - 54 \[Delta] + 23 \[Delta]^2)^2)/(4 \[Sqrt](( 36 (8 - 12 \[Delta] + 5 \[Delta]^2)^2)/(27 - 54 \[Delta] + 23 \[Delta]^2)^2 - ( 2 (110 - 124 \[Delta] + 53 \[Delta]^2))/( 3 (27 - 54 \[Delta] + 23 \[Delta]^2)) + (2^( 1/3) (544 - 856 \[Delta] + 1104 \[Delta]^2 - 568 \[Delta]^3 + 121 \[Delta]^4))/(3 (27 - 54 \[Delta] + 23 \[Delta]^2) (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^(1/3)) + (24640 - 58272 \[Delta] + 96288 \[Delta]^2 - 89456 \[Delta]^3 + 53952 \[Delta]^4 - 18096 \[Delta]^5 + 2662 \[Delta]^6 + \[Sqrt](-36827136 + 168210432 \[Delta] - 563162112 \[Delta]^2 + 1234040832 \[Delta]^3 - 2085654528 \[Delta]^4 + 2646715392 \[Delta]^5 - 2546553600 \[Delta]^6 + 1815350400 \[Delta]^7 - 890320896 \[Delta]^8 + 275516640 \[Delta]^9 - 47708352 \[Delta]^10 + 3449952 \[Delta]^11))^( 1/3)/(3 2^( 1/3) (27 - 54 \[Delta] + 23 \[Delta]^2))))), Inequality[0, Less, \[Delta], Less, Root[7 - 52 # + 152 #^2 - 238 #^3 + 224 #^4 - 114 #^5 + 23 #^6& , 1, 0]]]

I leave y on your own.

score 0 · Answer 3 · 2023-04-01T00:39:58.943

I completely reworked my answer in resounse to a comment.

Both a Solve and a Reduce version are given. No commentary this time though.

solution = Reduce[x == (1/3)*(2 + y - Sqrt[1 + y + y^2]) && 
     y == -((-2 + Sqrt[4 + 3*(-1 + \[Delta])^2*\[Delta]*(-2 + (-1 + x)^2*\[Delta])])/(3*(-1 + \[Delta])^2)) && 
     0 < y < \[Delta] < x < 1, {x, y}, Reals, Cubics -> True, Quartics -> True] /. And -> List;

upperLimit = N[solution[[1,5]]]

0.3591039032327827

x = Function[\[Delta], Evaluate[solution[[2,2]]]]

Function[\[Delta], Root[7 - 4*\[Delta] + 2*\[Delta]^2 + (-48 + 40*\[Delta] - 18*\[Delta]^2)*#1 + 
     (110 - 124*\[Delta] + 53*\[Delta]^2)*#1^2 + (-96 + 144*\[Delta] - 60*\[Delta]^2)*#1^3 + 
     (27 - 54*\[Delta] + 23*\[Delta]^2)*#1^4 & , 1]]

In[5]:=
y = Function[\[Delta], Evaluate[solution[[3,2]]]]
Out[5]=
Function[\[Delta], 2/(3*(-1 + \[Delta])^2) - (1/(3*(-1 + \[Delta])^2))*
    Sqrt[4 + 3*(-1 + \[Delta])^2*\[Delta]*
       (-2 + \[Delta]*(-1 + Function[\[Delta], Root[7 - 4*\[Delta] + 2*\[Delta]^2 + (-48 + 40*\[Delta] - 18*\[Delta]^2)*#1 + 
               (110 - 124*\[Delta] + 53*\[Delta]^2)*#1^2 + (-96 + 144*\[Delta] - 60*\[Delta]^2)*#1^3 + (27 - 54*\[Delta] + 
                 23*\[Delta]^2)*#1^4 & , 1]])^2)]]

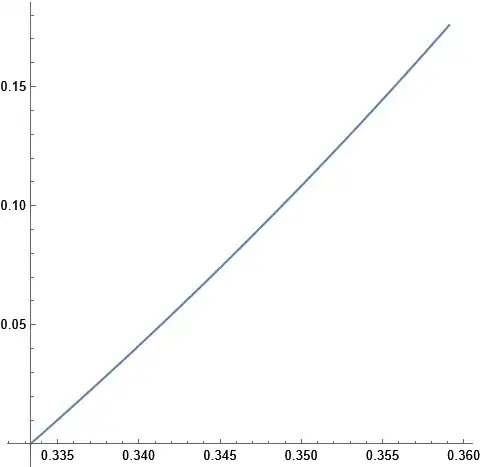
ParametricPlot[{x[\[Delta]], y[\[Delta]]}, {\[Delta], 2.^(-50), upperLimit}, PlotRange -> All, AspectRatio -> 1]

Mathematica graphics

ClearAll[x]; ClearAll[y]

solution = First[{x, y} /. Solve[x == (1/3)*(2 + y - Sqrt[1 + y + y^2]) && 
       y == -((-2 + Sqrt[4 + 3*(-1 + \[Delta])^2*\[Delta]*(-2 + (-1 + x)^2*\[Delta])])/(3*(-1 + \[Delta])^2)) && 
       0 < y < \[Delta] < x < 1, {x, y}, Reals, Cubics -> True, Quartics -> True]];

upperLimit = N[solution[[1, 2, 5]]]

0.3591039032327827

upperLimit == N[solution[[2,2,5]]]

True

x=\[Delta]|->Evaluate[solution[[1,1]]]

Function[\[Delta], (1/3)*(2 + Root[36*\[Delta]^2 - 8*\[Delta]^3 + (-144*\[Delta] + 16*\[Delta]^2 + 4*\[Delta]^3)*#1 + 
       (144 + 108*\[Delta] - 236*\[Delta]^2 + 124*\[Delta]^3 - 11*\[Delta]^4)*#1^2 + 
       (-216 + 432*\[Delta] - 194*\[Delta]^2 - 12*\[Delta]^3 + 6*\[Delta]^4)*#1^3 + 
       (81 - 324*\[Delta] + 474*\[Delta]^2 - 300*\[Delta]^3 + 69*\[Delta]^4)*#1^4 & , 1] - 
    Sqrt[1 + Root[36*\[Delta]^2 - 8*\[Delta]^3 + (-144*\[Delta] + 16*\[Delta]^2 + 4*\[Delta]^3)*#1 + 
         (144 + 108*\[Delta] - 236*\[Delta]^2 + 124*\[Delta]^3 - 11*\[Delta]^4)*#1^2 + 
         (-216 + 432*\[Delta] - 194*\[Delta]^2 - 12*\[Delta]^3 + 6*\[Delta]^4)*#1^3 + 
         (81 - 324*\[Delta] + 474*\[Delta]^2 - 300*\[Delta]^3 + 69*\[Delta]^4)*#1^4 & , 1] + 
      Root[36*\[Delta]^2 - 8*\[Delta]^3 + (-144*\[Delta] + 16*\[Delta]^2 + 4*\[Delta]^3)*#1 + 
          (144 + 108*\[Delta] - 236*\[Delta]^2 + 124*\[Delta]^3 - 11*\[Delta]^4)*#1^2 + 
          (-216 + 432*\[Delta] - 194*\[Delta]^2 - 12*\[Delta]^3 + 6*\[Delta]^4)*#1^3 + 
          (81 - 324*\[Delta] + 474*\[Delta]^2 - 300*\[Delta]^3 + 69*\[Delta]^4)*#1^4 & , 1]^2])]

y = Function[\[Delta], Evaluate[solution[[2,1]]]]

Function[\[Delta], Root[36*\[Delta]^2 - 8*\[Delta]^3 + (-144*\[Delta] + 16*\[Delta]^2 + 4*\[Delta]^3)*#1 + 
     (144 + 108*\[Delta] - 236*\[Delta]^2 + 124*\[Delta]^3 - 11*\[Delta]^4)*#1^2 + 
     (-216 + 432*\[Delta] - 194*\[Delta]^2 - 12*\[Delta]^3 + 6*\[Delta]^4)*#1^3 + 
     (81 - 324*\[Delta] + 474*\[Delta]^2 - 300*\[Delta]^3 + 69*\[Delta]^4)*#1^4 & , 1]]

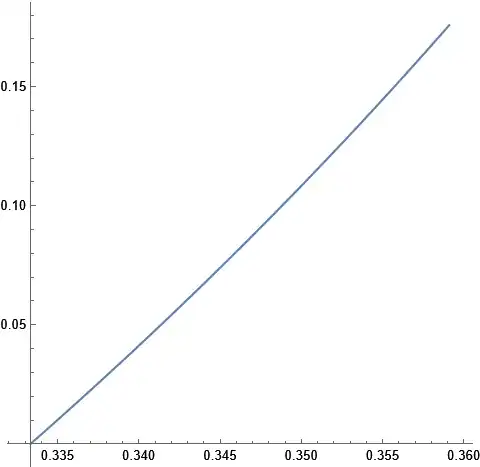
ParametricPlot[{x[\[Delta]], y[\[Delta]]}, {\[Delta], 2.^(-50), upperLimit}, PlotRange -> All, AspectRatio -> 1]

Mathematica graphics

The original answer so that you can see what I got wrong and right.

Avail the solution as a pure function with δ as a free variable:

solution = Evaluate[First[{x, y} /. Solve[x == (1/3)*(2 + y - Sqrt[1 + y + y^2]) && 
        y == -((-2 + Sqrt[4 + 3*(-1 + \[Delta])^2*\[Delta]*(-2 + (-1 + x)^2*\[Delta])])/(3*(-1 + \[Delta])^2)) && 0 < y < \[Delta] < x < 1, 
       {x, y}, Reals, MaxExtraConditions -> All, Cubics -> True, Quartics -> True]]] & ;

Make the solution into two argument function:

expression = Function[{\[Delta], parameter}, Append[solution[parameter], \[Delta]]]

3.Plot the three-dimensional function:

Mathematica graphics

Here are a few suggestions:

The Solve command used by you produces generic solutions and may use non-equivalent transformations. — user64494, Mar 31 '23 at 18:26
@user64494 I had checked. In this specific case, the results were equivalent allowing for the format differences of the answers. Did you notice these options: Reals, MaxExtraConditions -> All, Cubics -> True, Quartics -> True. These options avoid the "generic" solution issue. — , Apr 01 '23 at 00:00
Thanks,your answer really helped me a lot. Thank you for your patience in answering my questions. — zhongtianrachel, Apr 01 '23 at 05:47
I'm sorry to bother you.Now based on the original problem, I have a new problem which is too complicated to solve. I‘d appreciate some help. I edit my problem so that you can see it above. — zhongtianrachel, Apr 26 '23 at 10:23

How to plot the solutions of nonlinear equations with a parameter varies?

3 Answers3