The PDEs we are interested in solving using NDSolve is the vorticity-stream formulation of the 3D axisymmetric Navier-Stokes (Euler) equations (Ref.1 :T. Y. Hou, Potential singularity of the 3D Euler equations in the interior domain, arXiv:2107.05870): \begin{equation}\label{NSvorticityStreamD2} u_{t}+(-xf_{z}) u_{x}+(2f+xf_{x}) u_{z} =\nu \left(u_{xx} +u_{zz}+\tfrac{3}{x}u_{x}\right) +2uf_{z}\\ % w_{t}+(-xf_{z}) w_{x}+(2f+xf_{x}) w_{z} =\nu \left(w_{xx}+\omega_{zz}+\tfrac{3}{x}w_{x}\right)+2u u_{z},\\ % -w=\,\,\,\,\left(f_{xx} +f_{zz}+\tfrac{3}{x}f_{x} \tag{1}\right). \end{equation}
The initial conditions are \begin{equation}\label{InitialConditions} u(0,x,z)=\frac{12000(1-x^2)^{18}\sin(2\pi z)}{1+12.5\sin^2(\pi z)},\\ w(0,x,z)=f(0,x,z)=0 \tag{2}. \end{equation}
The boundary conditions are \begin{equation}\label{BoundaryConditionD2} u(t,\pm1,z)=f(t,\pm1,z)=w(t,\pm1,z)=0.\\ u(t,x,\pm \tfrac12)=f(t,x,\pm \tfrac12)=w(t,x,\pm \tfrac12)=0. \end{equation}
When I used the following NDSolve command
NDSolve[{PDE, IC, BC}, {u, w, f}, {t, 0, 1/10}, {x, -1, 1}, {z, -1/2, 1/2}]
I got the error message:
Infinite expression 1/0 encountered.
I will add Mathematica code tonight. Here is the Mathematica code:
PDE = {-2*u[t, x, z]*Derivative[0, 0, 1][f][t, x, z] +
Derivative[0, 0, 1][u][t, x, z]*
(2*f[t, x, z] + x*Derivative[0, 1, 0][f][t, x,
z]) - x*Derivative[0, 0, 1][f][t, x, z]*
Derivative[0, 1, 0][u][t, x, z] +
Derivative[1, 0, 0][u][t, x, z] == 0,
-2*u[t, x, z]*Derivative[0, 0, 1][u][t, x, z] +
Derivative[0, 0, 1][w][t, x, z]*
(2*f[t, x, z] + x*Derivative[0, 1, 0][f][t, x,
z]) - x*Derivative[0, 0, 1][f][t, x, z]*
Derivative[0, 1, 0][w][t, x, z] +
Derivative[1, 0, 0][w][t, x, z] == 0,
w[t, x, z] + Derivative[0, 0, 2][f][t, x, z] +
(3*Derivative[0, 1, 0][f][t, x, z])/x +
Derivative[0, 2, 0][f][t, x, z] == 0}
IC = {w[0, x, z] == 0, f[0, x, z] == 0,
u[0, x, z] == 12000(1 - x^2)^18
(Sin[2Piz]/(1 + (25/2)Sin[Piz]^2))}
BC = {w[t, x, 1/2] == 0, f[t, x, 1/2] == 0,
u[t, x, 1/2] == 0, w[t, x, -2^(-1)] == 0,
f[t, x, -2^(-1)] == 0, u[t, x, -2^(-1)] == 0,
w[t, 1, z] == 0, f[t, 1, z] == 0, u[t, 1, z] == 0,
w[t, -1, z] == 0, f[t, -1, z] == 0,
u[t, -1, z] == 0}
NDSolve[{PDE, IC, BC}, {u, w, f}, {t, 0, 1/10}, {x, -1, 1}, {z, -1/2, 1/2}]
From inspection, we know that if $u(0,x,z),w(0,x,z),f(0,x,z)$ are even in $x$, then the solution $u(t,x,z),w(t,x,z),f(t,x,z)$ will remain to be even in $x$. So the coordinate singular term $(1/x)u_x$ is nonsingular as $x\to 0$. NDSolve is not capable of figuring out this fact.
Any suggestions?
Best regards- Mike
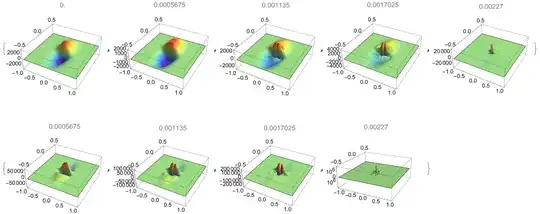
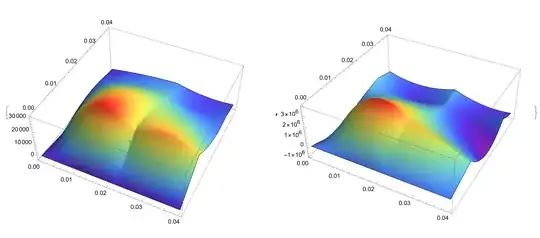
(3*Derivative[0, 1, 0][f][t, x, z])/xwith(3*Derivative[0, 1, 0][f][t, x, z])/Sqrt[x^2+eps]whereeps=0.00001or so. This alone does not solve your problem, since the warning: "Unable to find initial conditions that satisfy..." pops up. – Alexei Boulbitch Apr 04 '23 at 12:44Method -> {"MethodOfLines", "TemporalVariable" -> t, "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 50, "MinPoints" -> 50}}) – Michael E2 Apr 04 '23 at 14:42{x, -1, 0, 1}to{x, -1, 1}. – Michael E2 Apr 05 '23 at 00:36