Composition of functions

Question

I have a number of rotations computed by rot = RotationTransform[theta, point], and I would like to compose them to produce one function that is the composition of all the rotations. I need this function in a form that I can then use in, say, FindMinimum[].

I solved my problem by using TransformationMatrix[rot], multiplying all the matrices, and defining a function based on that. But it would be cleaner to create one function that is the composition of the others, rather than take the detour through matrices. Ideally I would input a list of `theta, point' values, and get back a function that is the composition of all those rotations.

I'd appreciate learning how to do this. Thanks!

Why don't you post the code for the functions your have. Then someone can suggest how to compose them. — DavidC, Mar 12 '12 at 15:49
Why would you not want to work with the matrices directly? Seems like a straightforward way to compose the combined rotation. — Yves Klett, Mar 12 '12 at 15:54
@David: I didn't want to bias the answers to my specific situation. The various rotations are computed in separate parts of the code, and only lashed together at the end. I would have to contrive an example to make it independent of my details. — Joseph O'Rourke, Mar 12 '12 at 17:15
@Yves: It works perfectly by multiplying matrices. I just thought that was an inelegant solution. — Joseph O'Rourke, Mar 12 '12 at 17:16
Ultimately, the matrices will get multiplied together, anyway. The question is whether or not you do it yourself. — rcollyer, Mar 12 '12 at 17:21
@Joseph Looks like several people were able to answer your question without having access to the specific functions. — DavidC, Mar 12 '12 at 21:13
@David If the more general question has a good answer, like in this case, it's more useful to have the more general question. The only problem is that the asker can't easily guess if a general solution is possible. :-) — Szabolcs, Mar 13 '12 at 05:32
I have learned much from this discussion--Thanks to everyone! — Joseph O'Rourke, Mar 14 '12 at 00:20

rcollyer · Accepted Answer · 2013-11-17T21:05:07.043

The function your looking for is Composition which does exactly what you would like it to do. For instance,

{rot1, rot2} = MapThread[RotationTransform, {{theta1,theta1},{point1,point2}}]
composed = Composition @@ %

Composition[
     RotationTransform[theta1, point1], 
     RotationTransform[theta1, point2]
  ]

which can then be used like rot1 and rot2 would, e.g. composed[ {x, y, z} ]. From some experiments, it seems that Composition will combine multiple TransformationFunction into a single TransformationFunction, e.g.

Composition[ RotationTransform[ Pi/2 ], RotationTransform[ Pi/2] ] ]

simplifies to

RotationTransform[ Pi ]

Here is a specific example using the following rotations

RotationTransform[Pi/2, {1, 0}]
RotationTransform[Pi/2, {1, 1}]
composed = Composition @@ {%, %%}

which gives the output (it's in picture form as the output is displayed using boxes):

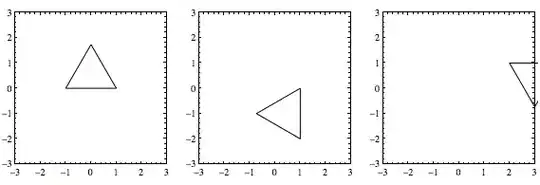
enter image description here

Now, applying them one at a time to a triangle, using the following code

FoldList[
  {EdgeForm[Black], White, #2[#1]} &, 
   Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}], 
  {# &, 
   GeometricTransformation[#, RotationTransform[Pi/2, {1, 0}]] &, 
   GeometricTransformation[#, RotationTransform[Pi/2, {1, 1}]] &}
][[2 ;;]] //
GraphicsRow[
 Graphics[#, Frame -> True, PlotRange -> {{-3, 3}, {-3, 3}}] & /@ # 
]&

gives

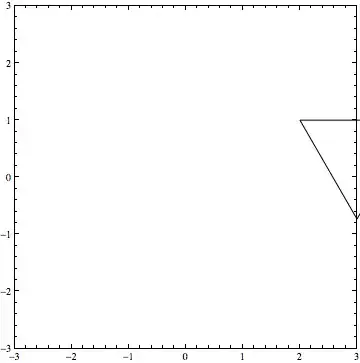
enter image description here

Using the composition directly via

Graphics[{
   EdgeForm[Black], White, 
   GeometricTransformation[
       Polygon[{{1, 0}, {0, Sqrt[3]}, {-1, 0}}], 
       composed]
  }, Frame -> True, PlotRange -> {{-3, 3}, {-3, 3}}]

gives the identical end result

enter image description here

Two things to note here. First, the functions are entered into Composition in reverse order of application, i.e. the first function to be applied is last, and the last function is first. Second, I made use of GeometricTransformation to apply the rotations to a Graphics primitive.

If you supply explicit values for the points like point1={u1, u2} the result is properly evaluated as well. — Yves Klett, Mar 12 '12 at 16:12
@YvesKlett actually, yes it does. You can combine any of the specializations of TransformFunction and they will be made into a single unit. — rcollyer, Mar 12 '12 at 16:14
Would you mind editing in an example with explicit rotation points? Should be quite instructive for future browsing. — Yves Klett, Mar 12 '12 at 16:41
@YvesKlett added an example with graphics for visual oriented people. — rcollyer, Mar 12 '12 at 17:16
@Hector, my use of TransformationFunction was deliberate. RotationTransform puts out a TransformationFunction which can then be composed. The change to transformationFunction loses that meaning. Reverting the edit. — rcollyer, Nov 17 '13 at 21:04
@rcollyer: My mistake. I did not know that Mathematica has TransformationFunction and TransformationFunctions with rather different uses and scopes. A Google search sent me here, so I assumed it was a mistake. — Hector, Nov 18 '13 at 13:41

Artes · Answer 2 · 2012-03-12T16:17:17.267

6

It seems you want a built-in function Composition. Having two functions f and g, where g depends on two arguments it works like this :

Composition[f, g] @@ {x, y}

f[g[x, y]]

E.g.

g[x_, y_] := ArcTan[x^2 y]
f[z_]     := 1/2 Tan[z]
Composition[f, g] @@ {x, y}

(x^2 y)/2

Composition works with many functions as well, e.g. :

Composition[f1, f2, f3, f4] @@ {x, y, z}

f1[f2[f3[f4[x, y, z]]]]

edited Mar 12 '12 at 16:17

answered Mar 12 '12 at 15:57

Artes

57,212
12
157
245

2

I wasn't aware that Composition will evaluate when transformation functions are passed to it. I think you should give an example using transformation functions to make this explicit. This is a special behaviour of Composition, specific to TransformationFunctions. – Szabolcs Mar 12 '12 at 16:06
1

Composition is also mentioned in the help under guide/GeometricTransforms. In this case it is a neat thing, but the GeometricTransformation framework can be a bit opaque IMHO. – Yves Klett Mar 12 '12 at 16:22
Thank you so much, two equivalent answers! – Joseph O'Rourke Mar 12 '12 at 17:17
@JosephO'Rourke You are welcome. – Artes Mar 12 '12 at 17:37
@Szabolcs Could you emphasize what are your objections if any ? – Artes Mar 12 '12 at 17:40
2

@Artes My meaning was that I was surprised and delighted to find that Compose[f,g] does indeed auto-simplify if f and g are TransformationFunctions, like rcollyer showed in his answer. I read your answer first and thought that it's less efficient than hand-multiplying the matrices and construction a new TranformationFunction from them. But I checked if Composition would actually evaluate, and surprise---it did! This only happens for TranformationFunction objects, and it is not obvious, so I asked you to include it (but it seems rcollyer did first). – Szabolcs Mar 13 '12 at 05:37
@Szabolcs If you check my example with g[x_,y_]:=2ArcTan[x^2 y] then you'll need to evaluate something like this Composition[f, g] @@ {x, y}// TrigExpand // Simplify, but I think this is a quite general issue, so in case of TranformationFunction similar things can be needed. – Artes Mar 13 '12 at 09:34
@Artes No, it's not an issue with TransformationFunctions, only with general functions. Composition[f, g] evaluates by itself when f and g are TransformationFunctions. This make a huge difference performance-wise when you apply the composed function to lots of arguments. I hope now it's more clear what I meant. – Szabolcs Mar 13 '12 at 09:36
@Szabolcs Ok, but in the context of the question it is not clear whether there are or not general functions. – Artes Mar 13 '12 at 09:44
To me, "I have a number of rotations computed by rot = RotationTransform[theta, point], and I would like to compose them" and "I solved my problem by using TransformationMatrix[rot], multiplying all the matrices" suggest that the OP is specifically interested in linear transformation functions (actually rotations) and wants to avoid the overhead of applying several rotations when they can be combined into a single one ... This is why I didn't answer with Composition. However, it was precisely your answer that made me realize that Composition is the best solution here after all. – Szabolcs Mar 13 '12 at 09:46

score 5 · Answer 3 · edited Apr 13 '17 at 12:56

One more thing that may be useful when working with Composition: to include a transformation that does nothing, use Identity.

You may ask why you'd ever need that. An example is given in this post for a shadow projection function: How to make a drop-shadow for a Graphics3D objects?

There is a transformation in the Composition that is supposed to be left out under certain conditions. The link also illustrates how much simpler Composition is than the alternative of adding vectors and multiplying matrices.

Composition of functions

3 Answers3

Linked