0

The differential equations I want to solve is

$$ \frac{\partial c_0(t)}{\partial t}=-\frac{1}{2} \kappa c_0(t)-\kappa \sum _{n=1}^N \alpha ^n c_0(t-\text{n$\tau $}) e^{i n \phi _{\tau }} \Theta (t-\text{n$\tau $}) $$ Here $\Theta(t)$ is the step function, $N$ is determined by $N=Integer[\frac{tmax}{\tau}]$. This equation has multipile time delays. By solving this equation, I think there may be chaos in this equation for certain parameters.

evofback[\[Tau]_, m_, \[Alpha]_, \[Phi]_, tlist_, cinitial_ : 1] := 
  Module[{\[Kappa] = 1, tm, sfeedback, c0, t}, tm = m*\[Tau]; 
   sfeedback = 
    NDSolveValue[{c0'[
        t] == -\[Kappa]/2*c0[t] - \[Kappa]*
         Sum[c0[t - n \[Tau]] UnitStep[t - n \[Tau]]*(\[Alpha])^(n)*
           Exp[n*I*\[Phi]], {n, 1, m}], 
                  c0[t /; t <= 0] == cinitial}, c0, {t, 0, tm}];
               Return[sfeedback[tlist]]];
ListLinePlot[evofback[2, 101, 1, 0, Subdivide[0., 101, 1001], 1], 
 PlotRange -> Full]

enter image description here

I want to calculate the chaotic nature of this equation. I know that there is already excellent Mathematica-based implementations for calculating Lyapunov Exponent Lyapunov exponent of Delay Differential Equation

But I don't know how to use it in my equation because this differential equaytion is different from these delay equations:

  • The time delay equation I am concerned with is that there are multiple time delays
  • Because of the step function limitation, although my equation has multiple time delays, it actually only needs one initial value instead of continuous initial values.So I myself don't think my equations need to be dealt with by discretizing the infinite dimension of time delay. Of course, in the actual implementation, I still have to provide a continuous infinite number of initial values, otherwise an warning will be reported, but I think this should be the reason for the equation writing in Mathematica.

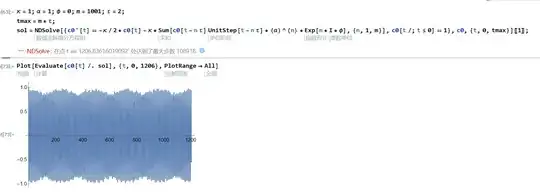
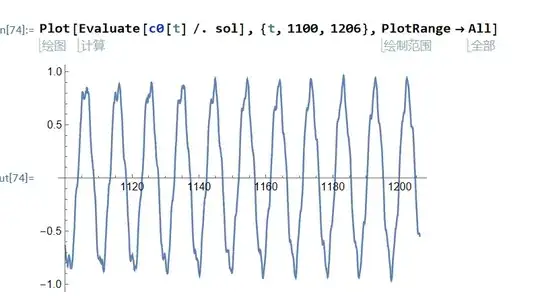
By ssolving the differential equations in a long time, we can see the following evolutions, I don't know whether there are chaos in this: enter image description here enter image description here

user64494
  • 26,149
  • 4
  • 27
  • 56
Knife Lee
  • 149
  • 7

1 Answers1

0

To calculate the Lyapunov exponents, first you need to get onto the attractor. In this case, I don't think there is one. Running it longer:

\[Kappa] = 1; \[Alpha] = 1; \[Phi] = 0; m = 101; \[Tau] = 2;
tmax = 2000;
sol = NDSolve[{
  c0'[t] == -\[Kappa]/2*c0[t] - \[Kappa]*
    Sum[c0[t - n \[Tau]] UnitStep[t - n \[Tau]]*(\[Alpha])^(n)*Exp[n*I*\[Phi]], {n, 1, m}],
  c0[t /; t <= 0] == 1}, c0, {t, 0, tmax}][[1]];

(* matching OP's output *)
Plot[Evaluate[c0[t] /. sol], {t, 0, 101}, PlotRange -> All]

enter image description here

(* looking over longer time *)
Plot[Evaluate[c0[t] /. sol], {t, 0, tmax}, PlotRange -> All]

enter image description here

Chris K
  • 20,207
  • 3
  • 39
  • 74
  • I forget to made constains on my differential equations, actually the tmax should be determined by m $t_{max}=m\tau$ – Knife Lee Apr 17 '23 at 03:18
  • As I understand it, Lyapunov exponents are defined as $t\to\infty$, so you can't have a $t_{max}$ – Chris K Apr 17 '23 at 03:43
  • Yes you are right, but I don't mean that $t_{max}$ can't be infinity, as $t\rightarrow \infty$ the corresponding $m=t_{max}/\tau$ should also be infinity, – Knife Lee Apr 17 '23 at 04:36
  • I see, but then the number of terms will also approach infinity. Seems tricky... – Chris K Apr 17 '23 at 05:05