How to optimize the code for deriving the standard equation of the Apollonian circle?

Question

The distance from a moving point in the plane to (0,0) is lambda times the distance from (a, 0). And lambda is not equal to 1. Find the equation

The standard equation form for a circle is:

(x - a)^2 + (y - b)^2 == r^2

The center coordinate of the circle is:{a,b} The radius is:r

Therefore, the equation form obtained according to the requirements is as follows:

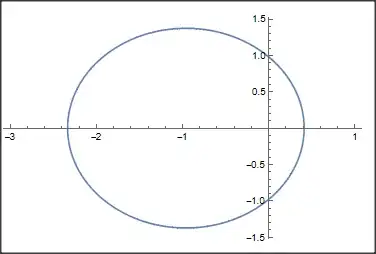
y^2 + (x - (a λ^2)/(-1 + λ^2))^2 == (
 a^2 λ^2)/(-1 + λ^2)^2

Clear["Global`*"]
expr = EuclideanDistance[{0, 0}, {x, 
    y}] == λ EuclideanDistance[{a, 0}, {x, y}]
eqn = Assuming[Element[{x, y, a, λ}, Reals], Simplify[expr]]
ApplySides[#^2 &, eqn]
eq = ApplySides[#^2 &, eqn] // Simplify
CompleteTheSquare::notquad = 
  "The expression is not quadratic in the variables `1`";
CompleteTheSquare[expr_] := CompleteTheSquare[expr, Variables[expr]]
CompleteTheSquare[expr_, Vars_Symbol] := 
 CompleteTheSquare[expr, {Vars}]
CompleteTheSquare[expr_, Vars : {__Symbol}] := 
 Module[{array, A, B, C, s, vars, sVars}, 
  vars = Intersection[Vars, Variables[expr]];
  Check[array = CoefficientArrays[expr, vars], Return[expr], 
   CoefficientArrays::poly];
  If[Length[array] != 3, Message[CompleteTheSquare::notquad, vars];
   Return[expr]];
  {C, B, A} = array; A = Symmetrize[A];
  s = Simplify[1/2 Inverse[A] . B, Trig -> False];
  sVars = Hold /@ (vars + s); A = Map[Hold, A, {2}];
  Expand[A . sVars . sVars] + Simplify[C - s . A . s, Trig -> False] //
    ReleaseHold]
Apply[Subtract, eq]
CompleteTheSquare[%, {x, y}]
ApplySides[#/Coefficient[%, y^2] &, % == 0]
CompleteTheSquare[% /. Equal -> Subtract, {x, y}] == 0
Fold[SubtractSides, %, Select[List @@ First@%, FreeQ[x | y]]]

Answer 1

The problem is quite similar to (if not a duplicate of)

How do I get my equation to have the form $(x-a)^2 + (y-b)^2 + (z-c)^2-d = 0$?

Based on chyanog's solution therein:

expr = 
 EuclideanDistance[{0, 0}, {x, y}] == λ EuclideanDistance[{a, 0}, {x, y}]
(* Sqrt[Abs[x]^2 + Abs[y]^2] == λ Sqrt[Abs[a - x]^2 + Abs[y]^2] *)
eqn = Assuming[{x, y, a, λ} ∈ Reals, Simplify@expr]
(* Sqrt[x^2 + y^2] == Sqrt[(a - x)^2 + y^2] λ *)
rule = Solve[ForAll[{x, y}, 
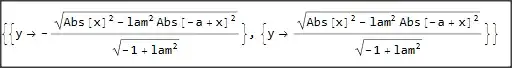
                    Apply[Subtract]@Map[#^2 &]@eqn == d ((x - aa)^2 + (y - b)^2 - c)], 
        {aa, b, c, d}][[1]]
(* {aa -> (a λ^2)/(-1 + λ^2), b -> 0, 
    c -> (a^2 λ^2)/(-1 + λ^2)^2, d -> 1 - λ^2} *)
(x - aa)^2 + (y - b)^2 == c /. rule
(* y^2 + (x - (a λ^2)/(-1 + λ^2))^2 == (a^2 λ^2)/(-1 + λ^2)^2 *)

Alternatively, based on Leonid's solution therein:

expr = EuclideanDistance[{0, 0}, {x, y}] == λ EuclideanDistance[{a, 0}, {x, y}]
(* Sqrt[Abs[x]^2 + Abs[y]^2] == λ Sqrt[Abs[a - x]^2 + Abs[y]^2] *)
eqn = Assuming[{x, y, a, λ} ∈ Reals, Simplify@expr]
(* Sqrt[x^2 + y^2] == Sqrt[(a - x)^2 + y^2] λ *)
mid = Collect[Apply[Subtract]@Expand@Map[#^2 &]@eqn, x | y]
(* -a^2 λ^2 + 2 a x λ^2 + x^2 (1 - λ^2) + y^2 (1 - λ^2) *)
mid2 = With[{pat = v : x | y}, 
  mid /. c1_ pat^2 + c2_ pat + c3_ :> (v + c2/c1/2)^2 - (c2/c1)^2/4 + Simplify[c3/c1]]
(* y^2 - (a^2 λ^4)/(1 - λ^2)^2 + (a^2 λ^2)/(-1 + λ^2) + (x + (a λ^2)/(1 - λ^2))^2 *)
With[{pat = v : x | y}, mid2 /. a_ + b_ /; FreeQ[b, x | y] :> a == -b] // Map@Simplify
(* y^2 + (x + (a λ^2)/(1 - λ^2))^2 == (a^2 λ^2)/(-1 + λ^2)^2 *)

Answer 2

We first define the points:

p = {x, y};
pa = {a, 0};
p0 = {0, 0};

Now the equation is:

eq = {Norm[p] == lam Norm[p - pa]};

We solve it for y to get the equation and define a function fy{x}:

Solve[eq, y]
fy[x_] = y /. Solve[eq, y];

For a test we define an numerical function fun[x] and plot it:

fun[x_] = fy[x] /. {lam -> 0.7, a -> 1.};
Plot[fun[x], {x, -3, 1}]

This is not a circle because of the AspectRatio. If we set AspectRatio-> Automatic we will get a circle:

Plot[fun[x], {x, -3, 1}, AspectRatio -> Automatic]