Revolution of a 2D graphics

Question

I would like to know how can we make a revolution around an axis of a 2D shape (a rectangle for example). I saw that there is the RevolutionPlot function but I can't manage to use it. I would also like the result to be solid. How to do ?

See https://mathematica.stackexchange.com/questions/283884/solid-of-revolution, https://mathematica.stackexchange.com/questions/59056/filling-the-empty-space-in-revolutionplot3d, and perhaps https://mathematica.stackexchange.com/questions/144989/filling-in-a-revolutionplot3d — Michael E2, Apr 21 '23 at 12:43

cvgmt · Accepted Answer · 2023-04-22T09:52:11.667

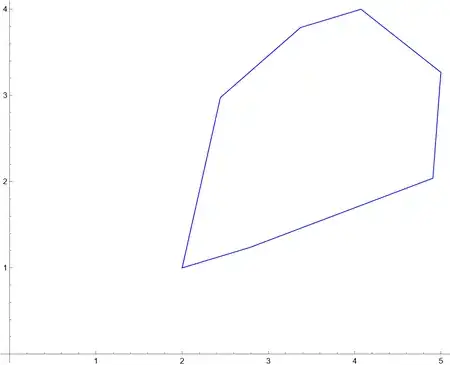
We can rotate a convex polygon.

SeedRandom[111];
reg = RandomPolygon[{"Convex", 7}, DataRange -> {{2, 5}, {1, 4}}];
Graphics[{EdgeForm[Blue], FaceForm[], reg}, Axes -> True, 
 AxesOrigin -> {0, 0}]

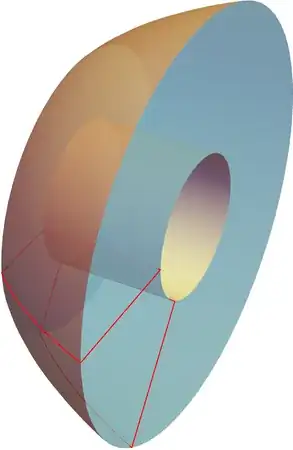
We rotate all of the sides of the convex polygon around the direction {0, 0, 1}

pairs = MeshPrimitives[BoundaryDiscretizeRegion@reg, 1][[;; , 
     1]] /. {x_Real, y_Real} :> {0, x, y};
ParametricPlot3D[
 RotationTransform[θ, {0, 0, 1}] /@ ({1 - t, t} . # & /@ 
     pairs) // Evaluate, {θ, 0, 2 π}, {t, 0, 1}, 
 MeshFunctions -> {#4 &}, Mesh -> {{π, 1.3 π}}, 
 MeshStyle -> Directive[Thick, Red], PlotPoints -> {60, 10}, 
 MaxRecursion -> 2, PlotStyle -> Directive[Opacity[.8], LightGreen], 
 Boxed -> False, Axes -> False]

The example in the comment of the question.

Clear["Global`*"];
f[x_] = 2 + Log[x];
g[x_] = 1;
reg = Plot[{f[x], g[x]}, {x, 1, E}, AspectRatio -> Automatic, 
    Filling -> {1 -> {2}}] // BoundaryDiscretizeGraphics;
pairs = MeshPrimitives[BoundaryDiscretizeRegion@reg, 1][[;; , 
     1]] /. {x_Real, y_Real} :> {x, y, 0};
ParametricPlot3D[
 RotationTransform[θ, {1, 0, 0}] /@ ({1 - t, t} . # & /@ 
     pairs) // Evaluate, {θ, 0, 2 π}, {t, 0, 1}, 
 MeshFunctions -> {#4 &}, Mesh -> {{π, 1.3 π}}, 
 MeshStyle -> Directive[Thick, Red], PlotPoints -> {60, 10}, 
 MaxRecursion -> 2, PlotStyle -> Directive[Opacity[.8], LightGreen], 
 Boxed -> False, Axes -> False]

But for any arbitrary graphics,for example,the text of font, it is still needs to find another way to deal with.

Revolution of a 2D graphics

1 Answers1