Symbolic Definite Integration

Question

How do I perform

Integrate[Sin[x]^2/(z^2 + R^2 - 2 zRCos[x])^(3/2), {x, 0, Pi}]

where z and R are constants. I would like if possible the result in terms of z and R.

Answer 1

At first, if one is not familiar with Mathematica syntax there is so called Free-Form input. These blog posts by Stephen Wolfram written when Mathematica 8 had been released discuss related issues extensively:

• The Free-Form Linguistics Revolution in Mathematica
• Programming with Natural Language Is Actually Going to Work

In a new cell one uses this shorthand = to start free-form input, copying the given command and evaluating it we get an appropriate form of ordinary Mathematica input and a bit later the result in terms of ConditionalExpression[ expr, cond] (the result == expr when the condition cond is satisfied):

Alternatively, one can converse free-form linguistics to inline Mathematica input ( shorthand Ctrl + =)

Then clicking on the result we get a correct input line. Now, even a complete beginner should get an idea what should be an appropriate input form, instead of * between symbolic variables one can use spaces as well (see e.g. Mathematical Typesetting guide).

When the syntax is not a problem anymore we could enhance our input.

Since we'd like to get a symbolic result it is resonable to add some assumptions (there is an option Assumptions in Integrate and other important functions in calculus, see a related post How to specify assumptions before evaluation? ) to speed up symbolic processing. In general, (if there are adequate built-in rewrite rules) we can expect the result in terms of ConditionalExpression. We can get rid of it with e.g. Refine[ ConditionalExpression[ expr, cond], cond], sometimes we might need Simplify or FullSimplify instead of Refine, for more complete discussion of simplification methods see What is the difference between a few simplification techniques?.

For the problem at hand we add assumptions that parameters z and R are real to avoid unnecessary and time-consuming symbolic processing, moreover we want to exclude z == R or z == -R since there would be a singularity in the integrand at x == 0 and x == Pi. For terse coding we could define a new function in terms of elliptic integrals of the first and the second kind:

f[z_, R_] = Integrate[ Sin[x]^2/(z^2 + R^2 - 2 z R Cos[x])^(3/2), {x, 0, Pi}, 
                       Assumptions -> z != -R && z != R && (z | R) ∈ Reals && z != 0]

(-(R + z)^2 EllipticE[(4 R z)/(R + z)^2] + (R^2 + z^2) EllipticK[(4 R z)/(R + z)^2]
  )/(R^2 z^2 Abs[R + z])

f[z, R] // TraditionalForm

We could visualize our symbolic expression:

Plot3D[ f[z, R], {R, 0.1, 3}, {z, 0.1, 3}, 
        PlotPoints -> 70, MaxRecursion -> 3, Exclusions -> z == R]

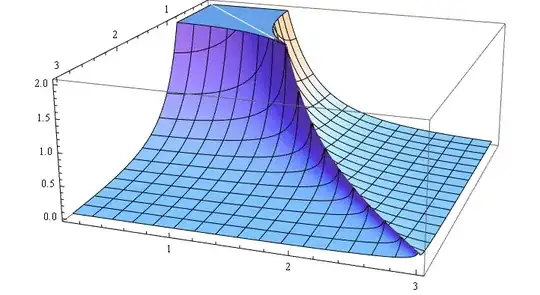
or with ContourPlot:

ContourPlot[ f[z, R], {R, 0, 3}, {z, 0, 3}, 
             PlotPoints -> 60, MaxRecursion -> 3, Contours -> 17, 
             ColorFunction -> "BlueGreenYellow"]