1

I have the following dataset:

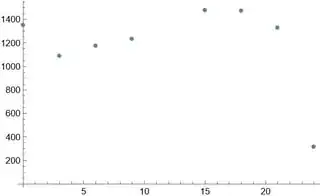
data = {{0, 1351.53}, {3, 1087.17}, {6, 1172.23}, {9, 1231.27}, {15, 1476.93}, {18, 1470.70}, {21, 1326.23}, {24, 316.80}}

which looks like

ListPlot[data]

enter image description here

I need to fit this dataset with one or two free parameters at most. I usually fist use FindFormula[data] to get a feeling how the fitting function should look like; however, here it doesn't seem to be helpful as I cannot make sense of the result. What are the other approaches to fit this dataset?

EDIT1

My first attempt, but it seems that I'm overfitting the data:

pp = Fit[data, {1, x^2, x^3}, x]

which gives

Show[ListPlot[data, PlotStyle -> Red], Plot[pp, {x, 0, 25}], PlotRange -> All]

enter image description here

EDIT2

Also, the dataset with the corresponding errors:

datae = {{0, Around[1351.53, 366.6818830176006]}, {3, Around[1087.17, 336.12935506041913`]}, {6, Around[1172.23, 302.7905271525735]}, {9, Around[1231.27, 257.5652603386826]}, {15, Around[1476.93, 10.45482344821443]}, {18, Around[1470.7, 57.16826042481958]}, {21, Around[1326.23, 175.39855567630354`]}, {24, Around[316.8, 45.14022596310301]}}

ListPlot[datae]

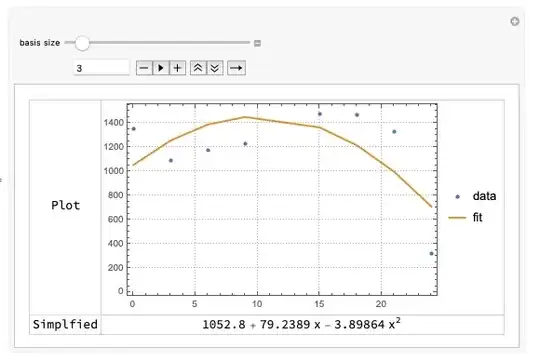
enter image description here

  • 1
    In order to meaningfully fit a model to a dataset there needs to be some pattern in the data... Can you tell us what process generated the data, and why you expect there to be a pattern? – Marius Ladegård Meyer May 02 '23 at 08:39
  • @Sara {1, x^2, x^3} you're missing an x^1 in there. There is no clear cut answer for how many parameters you should choose. You may want to consider using FitRegularization->{"LASSO", 1.0} where 1.0 is up to you. This will try to minimize the L1 norm of the parameters which tries to keep parameters small. Also you could try the RANSAC algorithm like in my answer here which gives you a more robust estimation and downplays the effects of outliers. More simply, you could just drop that last point from the data and fit a line. – flinty May 02 '23 at 10:21
  • @Sara I don't think it is - you should have an $x$ term in there unless you have a very good reason not to suspect an x^1 term in the underlying process this data comes from. – flinty May 02 '23 at 12:45
  • "I'm still studying the involved mechanisms and I don't know if there is a pattern or not;" That's a very reasonable statement. So why not just show the points and the error bars? Otherwise, (based on the comments here and in the current answer) it appears that you're using the "I'll know it when I see it" decision rule. A fit can wait until either there's more data or some theoretical model is justified. – JimB May 02 '23 at 13:44
  • You only have 8 data points and the source of your error values hasn't been explained. While those errors might be accurately associated with measurement error, that doesn't address any additional lack-of-fit error (especially as the underlying curve is unknown). And, to repeat: you only have 8 data points. One shouldn't expect magic to happen. And I get that 8 data points might have been very expensive to obtain and that this can be cutting-edge science. It's simply that there's no statistical method that will fix having only 8 data points. – JimB May 02 '23 at 13:55

1 Answers1

3

Try using Manipulate over the parameters of interest or possible parameters.

Below is given an example with the number of functions in a certain basis. But, of course, other bases or parameters can be programmed and used.

Manipulate[
 fFunc = 
  Fit[data, Table[ChebyshevT[i, Rescale[x, MinMax[data[[All, 1]]], {-1, 1}]], {i, 0, n - 1}], x];
 Grid[{{"Plot",
    ListPlot[{data, {#, fFunc /. x -> #} & /@ data[[All, 1]]}, 
     Joined -> {False, True}, PlotLegends -> {"data", "fit"}, 
     PlotStyle -> {Thin, Thick}, PlotTheme -> "Detailed", 
     ImageSize -> Medium]},
   {"Simplfied", Simplify[fFunc]}},
  Dividers -> All, FrameStyle -> LightGray
  ],
 {{n, 3, "basis size"}, 1, 40, 1, Appearance -> "Open"}
]

enter image description here

Anton Antonov
  • 37,787
  • 3
  • 100
  • 178
  • @Sara Please run the posted code and use the slider -- you will get better fits. Also, try replacing the Chebysev basis with your own basis of functions. With more data points you will start seeing the overfitting effects. – Anton Antonov May 02 '23 at 11:32
  • Well, I would rather use Quantile Regression with B-splines instead of Fit with polynomials (with infinite support). (See the section "Properties and Relations" and in link above.) – Anton Antonov May 02 '23 at 11:45
  • "Does this mean that at the end this regression also gives us polynomials?" -- Using B-spline basis we get piecewise polynomials. – Anton Antonov May 02 '23 at 11:57